Courbe paramétrée polaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Phaco
- Messages: 5
- Enregistré le: 13 Aoû 2017, 13:34
-
 par Phaco » 25 Aoû 2017, 17:23
par Phaco » 25 Aoû 2017, 17:23
bonjour,
je dois faire l'étude d'une fonction polaire P(teta)=1+cos( teta)
mais j'avoue être un peu paumé.
j'ai un peu compris pour une fonction cartésienne, mais j'ai plus de mal avec la trigo.
est-ce possible de m'orienter et m'expliquer ?
merci à vous

-
Phaco
- Messages: 5
- Enregistré le: 13 Aoû 2017, 13:34
-
 par Phaco » 25 Aoû 2017, 17:46
par Phaco » 25 Aoû 2017, 17:46
j'ai trouvé cette démo, mais j'ai du mal à comprendre.
- Fichiers joints
-

- courbe polaire.PNG (23.37 Kio) Vu 712 fois

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Aoû 2017, 17:51
par zygomatique » 25 Aoû 2017, 17:51
salut
ben tu as toute la démo ... que te faut-il de plus ?
remarquer que r(t) = 1 + cos t est une fonction définie et positive sur R par définition de la fonction cos ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 25 Aoû 2017, 18:06
par MJoe » 25 Aoû 2017, 18:06
Bonjour,
D'après la démo que tu as trouvé, tu vois que l'on étudie la fonction

sur
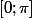
.
Soit
=1+cos\theta)
La dérivée est égale à :
=-sin\theta)
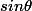
est positif sur
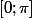
donc la dérivée est négative sur
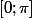
.
D'où le tableau de variation que tu as trouvé.
Voici un exemple de courbe représentative :

MJoe.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Aoû 2017, 18:18
par zygomatique » 25 Aoû 2017, 18:18
pas besoin de dérivée pour donner les variations de la fonction cos ... qui doivent être connues en post-bac ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 25 Aoû 2017, 18:31
par MJoe » 25 Aoû 2017, 18:31
Tout à fait mais bon il y a tellement de choses qui devraient être connues en post-bac et qui sont "oubliées" dans les faits.

MJoe.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 25 Aoû 2017, 18:48
par pascal16 » 25 Aoû 2017, 18:48
On peut ausi voir cette courbe sous la forme :
x=(1+cos(o))*cos(o)
y=(1+cos(o))*sin(o)
les dérivées en x et y donnent les mins et max.
la courbe est une cardoïde :
https://fr.wikipedia.org/wiki/Cardio%C3%AFdeIl faut ensuite étudier le point de rebroussement (1ere espèce).

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 25 Aoû 2017, 18:53
par MJoe » 25 Aoû 2017, 18:53
Bonjour,
Oui, je n'avais pas bien lu le sujet du topic !
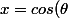*P(\theta)=cos(\theta)*(1+cos(\theta)))
et
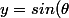*P(\theta)=sin(\theta)*(1+cos(\theta)))
MJoe.
-
Phaco
- Messages: 5
- Enregistré le: 13 Aoû 2017, 13:34
-
 par Phaco » 25 Aoû 2017, 20:44
par Phaco » 25 Aoû 2017, 20:44
merci beaucoup.
j'imagine que ça doit vous paraître "simple" ou évident.
mais je suis en cours de remise à niveau, après presque 20ans après mon BTS, c'est pas forcement rapide de retrouver les automatismes

vous risquez de me revoir souvent, j'espère monter en compétences rapidement.

-
MJoe
- Membre Relatif
- Messages: 295
- Enregistré le: 19 Juil 2017, 06:26
- Localisation: Saint-Nazaire
-
 par MJoe » 26 Aoû 2017, 17:34
par MJoe » 26 Aoû 2017, 17:34
Bonjour,
Nous avons tous été débutants, à nos débuts.
Bon travail à vous.
MJoe.

-
Phaco
- Messages: 5
- Enregistré le: 13 Aoû 2017, 13:34
-
 par Phaco » 28 Aoû 2017, 08:40
par Phaco » 28 Aoû 2017, 08:40
j'ai lu sur quelques page internet, il est nommé des "branches infinies".
ça correspond à quoi exactement ?
et encore une question "bête",quelle est la différence entre
l'équation polaire
P(x)=1+cosx
et l'équation paramétrée
x=(cosx)(1+cosx)
y=(sinx)(1+cosx)
par différence, j'entend quand est-ce que l'on utilise l'une ou l'autre ?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 28 Aoû 2017, 12:53
par pascal16 » 28 Aoû 2017, 12:53
C'est la même représentation dans deux repères différents du plan.
Mais :
en électronique, ce sont les notions d'angle et d'amplitude qui priment (Nyquist et autre), la courbe polaire et l'analyse en polaire est la plus adaptée.
en Math, la version classique permet de mieux comprendre les choses
en mécanique, c'est la courbe paramétrée par le temps qui va donner les inerties, vitesses et accélérations.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités

