Bonjour
@Yezu c'est l'inclusion inverse qu'il veut démontrer. C'est à dire que pour tout (x,y,z) appartenant à S il existe
 \in R^2)
t.q
=(x(u,v),y(u,v),z(u,v)))
@aispor Pour résoudre ton problème tu considères un élément quelconque
 \in S.)
C'est à dire que
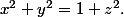
Nécessairement on a z=2v-1 et donc
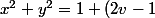^2=(\sqrt{2} v)^2+(\sqrt{2}(1- v))^2)
Posons
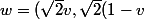))
. L'égalité précédente signifie que les vecteurs (x,y) et w ont même norme.
Il existe donc une rotation d'angle u, de matrice notée R(u) tel que
^t=R(u) w^t)
Cette dernière identité s'écrit aussi x=x(u,v), y=y(u,v) (où ici j'ai repris les notations de Yezu)
Ceci répond à ta question et avec le travail deYezu ça répond à toute la question.


