Couple solution d'un polynome

[wall]

Bonjour,

J'ai besoin d'aide pour venir à bout d'un calcul.

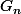
[INDENT]Je dois étudier les couples (, ) vérifiant
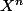
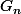
() : + = 1 avec n entier naturel non nul.

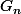
Je dois déduire l'existence de (, ) d'après le calcul de .[/INDENT]

J'ai dis que = (bornes de k=0 à 2n-1)

Après je voulais diviser la somme avec d'une part de k=0 à n-1 + de k=n à 2n-1.

Mais je ne vois pas comment continuer ... Avez-vous une piste ? Un changement d'indice judicieux peut etre ?

Bonne journée

[jlb]

tu as fini!! dans ta première somme, tu peux factoriser par X^n et dans la 2ème par (1-X)^n!!

[wall]

J'ai donc = (bornes de k=0 à 2n-1) + (bornes de k=n à 2n-1)

Par contre pour la seconde somme je voudrai commencer à k=0 et non à k=n Je peux faire quel changement d'indice ?

[jlb]

J'ai donc = (bornes de k=0 à 2n-1) + (bornes de k=n à 2n-1)

Par contre pour la seconde somme je voudrai commencer à k=0 et non à k=n Je peux faire quel changement d'indice ?

un truc comme j=k-n devrait aller!!!