Densite d'un couple (min/max)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zenaf
- Membre Naturel
- Messages: 98
- Enregistré le: 18 Jan 2007, 15:21
-
 par zenaf » 25 Fév 2010, 19:09
par zenaf » 25 Fév 2010, 19:09
Bonjour.
Je vous présente mon problème:
On définit

des variables aléatoires réelles indépendantes de même loi.
On pose

Pour calculer la densité (supposée par hypothese) du couple
)
je commence par calculer la fonction de répartition du couple:
}=P(S\leq x,I \leq y)=P(S\leq x) *P(I \leq y | S \leq x))
Alors je distingue deux cas:
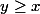
Et alors j'obtiens
=1)

Et alors
= P(I \leq y)=F_I(y))
Ce qui finalement nous donne
}=P(S\leq x,I \leq y)=F_S(x)(\mathbb{1}_{[y \geq x]} (x,y)+F_I(y)\mathbb{1}_{[y < x]}(x,y)))
Seulement j'ai des doutes sur ce calcul. Pourrait t'on me le confirmer ou me l'infirmer?
Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Fév 2010, 00:37
par Ben314 » 26 Fév 2010, 00:37
Salut,
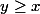
=>
=1)
est OK
Mais
= P(I \leq y))
est FAUX :
Si je te dit que j'ai jeté trois dés et que le plus grand est un 1, croit tu que la proba que le le plus petit est un 1 est la même que si je t'avais dit que le plus grand est un 6 ?
Aprés, pour la bonne réponse, je pense qu'il faut réellement écrire la densité du n-uplet (X1,X2,...Xn) et l'intégrer sur le domaine qui corespond à min(Xi)<x ; max(Xi)<y pour trouver la fonction de répartition de (Min,Max).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par alavacommejetepousse » 26 Fév 2010, 07:51
par alavacommejetepousse » 26 Fév 2010, 07:51
bonjour le plus simple est de passer par
P(I > y , S< x)
-
zenaf
- Membre Naturel
- Messages: 98
- Enregistré le: 18 Jan 2007, 15:21
-
 par zenaf » 27 Fév 2010, 19:21
par zenaf » 27 Fév 2010, 19:21
D'accord. J'ai eu
=P(S \leq x)-P(S \leq x,I >y))
et du coup je trouve
=F_S(x)-(F(x)-F(y))^n \mathbb{1}_{x>y})
Cela est t'il correct ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Fév 2010, 20:30
par Ben314 » 27 Fév 2010, 20:30
Ca me parrait parfaitement correct.
Il te reste à évaluer la loi de répartition du Max.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
