Oui, j'ai bien compris maintenant :
De manière général, si :

est un corps.

est un élément algébrique sur

.

est une extension de

tel que :
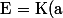 $)
.
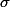
:
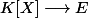
.
 $)
alors :
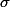
est un homomorphisme de corps et
 = (Irr(a,K)) $)
avec :
 $)
: le polynome minimal de

sur

.
et on a la décomposition suivante :

:
 $)
( projection canonique )

et

:
) \longrightarrow E $)
( isomorphisme de corps )
 $)
c'est à dire:
) \simeq E $)
Alors si on applique ça à notre exemple precedent, on trouve que :
 \simeq C $)
.
En effet:
On considère le corps

.

est algébrique sur

.
Soit
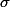
l'application définie par :
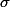
:
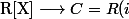 $)
 $)
.
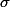
est un homomorphisme de corps ( c'est evident ).
et
 = (X^{2}+1) $)
avec :

le polynôme minimal de

sur

.
Par conséquent :

( Isomorhisme de corps ) telle que :

:
 \longrightarrow C $)
.
d'où :
 \simeq C $)
Revenons maintenant à notre application de départ:
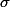
:
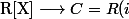 $)
.
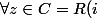 \exists a,b \in R $)
:

alors :
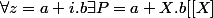
tel que :
 = \sigma(a + X.b) = (a +X.B)(i) = P(i) =a + i.b $)
.
On a la surjection canonique suivante :

:
 $)
tel que :
 = \bar{a+X.b} \in R[X]/(X^{2}+1) $)
.
Donc :
 = \{ \bar{a+X.b} / (a,b) \in R \} = \{ (X^{2}+1) + a+X.b / (a,b) \in R \} $)
.
Maintenant, il faut justifier, que pour tous polynome

de

:

est contenu necessairement dans une classe de
 $)
:

:
 $)
c'est à dire :

:
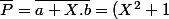 + a+X.b $)
.
En effet :

:

.
la division euclidienne de

par

implique que :

tel que :
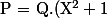 + R $)
avec :
 < 2 $)
donc

s'ecrit:

avec :

. D'où:
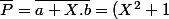 + a+X.b $)
...
Bref : le correspondant de

dans
 $)
est

...
Voilà ... !! :zen: