Corps engendré par une partie !
Bonjour:
j'ai une question à vous poser concernant un théorème et sa démonstration que j'ai du mal à comprendre.
voiçi le théorème :
 est un corps infini.
est un corps infini.
Si l'ensemble intermediaire entre et
et  est fini et si
est fini et si  $) alors
alors  est une extension simple de
est une extension simple de  .
.
voiçi la démonstration:
Considerons l'ensemble des corps intermédiaire entre est
est  de la forle
de la forle  $) où
où  . Cet ensemble est fini.
. Cet ensemble est fini.
Comme est infini , il existe deuc éléments distincts
est infini , il existe deuc éléments distincts  et
et  de
de  tel que:
tel que:
 = K(a_{1} + u.a_{2}) = L $) .
.
Nous avons :.a_{2} = (a_{1} + t.a_{2}) - (a_{1} + u.a_{2}) \in L $) et
et  car
car  .
.
Nous avons aussi: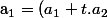 - t.a_{2} \in L $) .
.
Il en resulte que: = K(a_{1} , a_{2}) = E $) .
.
Par conséquent: est une extension simple de
est une extension simple de  .
.
Voiçi les passages que j 'ai pas compris:
1) Comment ça se fait que l'ensemble des corps intermediaire de la forme $) est fini alors que
est fini alors que  est infini et
est infini et  .
.
et merçi inifiment !!!
j'ai une question à vous poser concernant un théorème et sa démonstration que j'ai du mal à comprendre.
voiçi le théorème :
Si l'ensemble intermediaire entre
voiçi la démonstration:
Considerons l'ensemble des corps intermédiaire entre
Comme
Nous avons :
Nous avons aussi:
Il en resulte que:
Par conséquent:
Voiçi les passages que j 'ai pas compris:
1) Comment ça se fait que l'ensemble des corps intermediaire de la forme
et merçi inifiment !!!
Bonjour::
j'ai une question à vous poser concernant un théorème et sa démonstration que j'ai du mal à comprendre.
voiçi le théorème :
 est un corps infini.
est un corps infini.
Si l'ensemble intermediaire entre et
et  est fini et si
est fini et si  $) alors
alors  est une extension simple de
est une extension simple de  .
.
voiçi la démonstration:
Considerons l'ensemble des corps intermédiaire entre est
est  de la forle
de la forle  $) où
où  . Cet ensemble est fini.
. Cet ensemble est fini.
Comme est infini , il existe deuc éléments distincts
est infini , il existe deuc éléments distincts  et
et  de
de  tel que:
tel que:
 = K(a_{1} + u.a_{2}) = L $) .
.
Nous avons :.a_{2} = (a_{1} + t.a_{2}) - (a_{1} + u.a_{2}) \in L $) et
et  car
car  .
.
Nous avons aussi: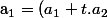 - t.a_{2} \in L $) .
.
Il en resulte que: = K(a_{1} , a_{2}) = E $) .
.
Par conséquent: est une extension simple de
est une extension simple de  .
.
Voiçi les passages que j 'ai pas compris:
1) Comment ça se fait que l'ensemble des corps intermediaire de la forme $) est fini alors que
est fini alors que  est infini et
est infini et  .
.
et merçi inifiment !!!!
j'ai une question à vous poser concernant un théorème et sa démonstration que j'ai du mal à comprendre.
voiçi le théorème :
Si l'ensemble intermediaire entre
voiçi la démonstration:
Considerons l'ensemble des corps intermédiaire entre
Comme
Nous avons :
Nous avons aussi:
Il en resulte que:
Par conséquent:
Voiçi les passages que j 'ai pas compris:
1) Comment ça se fait que l'ensemble des corps intermediaire de la forme
et merçi inifiment !!!!
La question :
La réponse :
barbu23 a écrit:.
Voiçi les passages que j 'ai pas compris:
1) Comment ça se fait que l'ensemble des corps intermediaire de la formeest fini alors que
est infini et
.
et merçi inifiment !!!!
La réponse :
barbu23 a écrit:.
voiçi le théorème :est un corps infini.
Si l'ensemble des corps intermediaires entreet
est fini et si
alors
est une extension simple de
.
barbu23 a écrit:2) Pourquoi a-t-on :tels que:
et
.
Dans
Resalut:
Le théorème dit:
Une extension finie de
de  est simple si et seulement si l'ensemble des corps intermédiaires entre
est simple si et seulement si l'ensemble des corps intermédiaires entre  et
et  est fini.
est fini.
Ensuite on donne un exemple et on dit : = Q(\sqrt{2}+\sqrt{3}) $) .
.
Ma question est :
1) Comment généralement, on arrive à détérminer le nombre de corps intermédiaires entre un corps et un extension
et un extension  .
.
2) Comment prouver que : = Q(\sqrt{2}+\sqrt{3}) $) .
.
et merçi infiniment !!
Le théorème dit:
Une extension finie
Ensuite on donne un exemple et on dit :
Ma question est :
1) Comment généralement, on arrive à détérminer le nombre de corps intermédiaires entre un corps
2) Comment prouver que :
et merçi infiniment !!
1) Pour les "bonnes" extensions E de K, c'est l'objet de la théorie de Galois que de trouver les corps intermédiaires. Dans l'exemple, il y en a trois.
2)L'inclusion droite-gauche est claire. Dans l'autre sens, cherche à fabriquer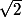 à partir de
à partir de  (Tu es bon pour élever ce dernier au carré, au cube et même à l'exposant 4 je pense, puis tu combines avec des coefs rationnels : très bon exercice.
(Tu es bon pour élever ce dernier au carré, au cube et même à l'exposant 4 je pense, puis tu combines avec des coefs rationnels : très bon exercice.
2)L'inclusion droite-gauche est claire. Dans l'autre sens, cherche à fabriquer
Yos:
En détail :
1) Pour montrer que : \subset Q(\sqrt{2}+\sqrt{3}) $) il faut montrer que :
il faut montrer que :  $) et
et  $) .
.
c'est à dire que : et
et  et chaque rationnel dans
et chaque rationnel dans  peut s'ecrire comme combinaisons des éléments de
peut s'ecrire comme combinaisons des éléments de  $) , c'est à dire comme combinaisons des rationnels de
, c'est à dire comme combinaisons des rationnels de  et de
et de  .
.
2) Pour montrer que : \subset Q(\sqrt{2},\sqrt{3}) $) , il faut montrer que :
, il faut montrer que :  $) et
et  $) .
.
c'est à dire que : et chaque rationnel dans
et chaque rationnel dans  peut s'ecrire comme combinaisons des éléments de
peut s'ecrire comme combinaisons des éléments de  $) , c'est à dire comme combinaisons des rationnels de
, c'est à dire comme combinaisons des rationnels de  et de
et de  et
et  .
.
Voilà.. Voilà.. , J'ai réfléchi un peu pour arriver à ça, c'est ce que je cherchais exactement ...!!! Mais la suite, je ne suis pas sûr comment la faire:
Par exemple pour 1) : on veut montrer que $) avec les
avec les  opérations :
opérations : 
On a :^{2} = 5 + 2.\sqrt{2}.\sqrt{3} $)

^{2} - 5}{2.\sqrt{3}} $) .
.
^{2} - 5}{2.\sqrt{3}} $) .
.
 :
:  .
.
donc : \subset Q(\sqrt{2}+\sqrt{3}) $) .
.
Maintenant pour : \subset Q(\sqrt{2},\sqrt{3}) $) .
.
 avec :
avec : 
 :
: 
d'où le résultat !
merçi yos !!
En détail :
1) Pour montrer que :
c'est à dire que :
2) Pour montrer que :
c'est à dire que :
Voilà.. Voilà.. , J'ai réfléchi un peu pour arriver à ça, c'est ce que je cherchais exactement ...!!! Mais la suite, je ne suis pas sûr comment la faire:
Par exemple pour 1) : on veut montrer que
On a :
donc :
Maintenant pour :
d'où le résultat !
merçi yos !!
Il y a des trucs justes dans le dernier message. Dans les précédents tu t'égares.
Le fait que) ou que
ou que ) est tout à fait évident.
est tout à fait évident.
De même il est clair que) et donc
et donc  \subset Q(\sqrt2,\sqrt3)) .
.
La seule chose moins immédiate, c'est l'inclusion inverse : \subset Q(\sqrt2+\sqrt3)) . Et pour celle-là, il suffit de prouver que
. Et pour celle-là, il suffit de prouver que ) et
et ) .
.
Tu peux poser , et voir que
, et voir que ^2=3) puis
puis  et enfin
et enfin  qui prouve que
qui prouve que ) .
.
Question : comment tu prouves l'irréductibilité de ton polynôme dans ton message 83?
Le fait que
De même il est clair que
La seule chose moins immédiate, c'est l'inclusion inverse :
Tu peux poser
Question : comment tu prouves l'irréductibilité de ton polynôme dans ton message 83?
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
