Corps des rationnels

[ludo56]

Bonjour,

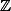
Je viens de montrer que : --> est un monomorphisme d'anneaux.
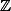
J'identifie alors à ().
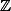
Je ne vois pas alors comment prouver que est un surcorps de .
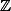
Merci d'avance pour votre aide!

[Ben314]

Heuuu....
Je comprend pas bien la question (je sais pas trop comment tes objets sont définis).
Il me semble que Q est un corps (on le construit surtout pour ça...) et tu vient de voir que l'on peut voir Z comme une partie de Q. Je sais pas quoi dire de plus...
A part peu être que d'écrire que Q est un "surcorps" de Z, ça donne assez franchement l'impression que Z était déjà un corps, ce qui n'est pas...

[barbu23]

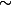
avec la relation d'quivalence definie par :
:
:happy3:
Je t'invite d'abord, à lire un petit cours sur ce qu'est la localisation d'un anneau en general ! ensuite, appliquer cette localisation à
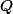
:happy3:

[ludo56]

Bonjour et merci. Pour le cours concernant la localisation,je n'ai pas de problèmes.J'ai surement était un peu vite.
Alors est définit par .
Quand je dis surcorps,c'est pour dire que Q est un corps qui contient Z et pour lequel Z est un sous anneau (il est vrai que je ne suis pas certain que l'appellation surcorps soit justifiée,désolé).Et mon problème se situe au dernier point.Pour montrer que Z est un sous anneau,on utilise l'identification via le morphisme mais je ne vois pas vraiment..

[Ben314]

Même le "dernier point", je vois pas trop ce qu'il y a à démontrer :
Ton morphisme est injectif donc réalise un isomorphisme de Z sur ce qui évidement prouve que est un anneau...