Bonjour! J'aimerais savoir si quelqu'un pouvait m'aider à prouver la convergence de la série suivante: (elle a l'air accessible kom ça, mais je bloc completement)
On a k un entier naturel et x un réel appartenant à [0,1[
Il faut alors montrer la convergence de la série de terme général
(n puissance k)(x puissance n)
avec n variant de 0 à + l'infini...
:mur:
merci d'avance!!!!!
PS: je sui dsl mais je c pas vraiment comment trouver les symbol mathématiques corrects pour les puissance, les symbol somme et infini...
Convergence d'une série
8 messages
- Page 1 sur 1
par yos » 01 Nov 2006, 16:59
Que dis ton cours?
Pour étudier la nature d'une série à termes positifs, on la compare à des séries connues.
C'est ce que je viens de faire. Dans ce cas précis, la partie polynomiale en n qu'est n^k est négligeable devant la partie exponentielle en n qu'est x^n (lorsque n tend vers + infini). C'est ce que je mets en évidence avec cet artifice (assez puéril ma foi) qui consiste à écrire que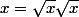
.
Le fait que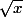
est lui aussi dans [0,1[ permet d'écrire que 
tend vers 0 quand n tend vers + infini, et donc que 
dés que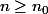 
. Tu as donc une majoration de 
par le terme général d'une série convergente (série géométrique).
Pour étudier la nature d'une série à termes positifs, on la compare à des séries connues.
C'est ce que je viens de faire. Dans ce cas précis, la partie polynomiale en n qu'est n^k est négligeable devant la partie exponentielle en n qu'est x^n (lorsque n tend vers + infini). C'est ce que je mets en évidence avec cet artifice (assez puéril ma foi) qui consiste à écrire que
Le fait que
re merci merci!!
par coroll » 01 Nov 2006, 17:46
Ca y est j'ai compris! merci beaucoup c'est vraiment gentil de ta part!!!
Re problème
par coroll » 06 Nov 2006, 19:34
En fait, je viens de relire très attentivement la démonstration que tu as faite. Je suis en prépa hec option éco, et j'ai du mal à comprendre les étapes.... Je suis désolée, mais je ne vois pas en quoi il y a négligeabilité et en quoi on abouti à une majoration, ni par quelle majoration. Je suis encore dsl, mais j'ai du mal....
par yos » 06 Nov 2006, 19:46
Pour ta première question, je vois mal ce qui te bloque. Il s'agit de théorèmes qu'on voit en terminale et qui disent que la fonction exponentielle "l'emporte" sur les fonctions puissances en + l'infini. Ici la puissance c'est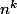 
et l'exponentielle c'est 
(qu'on peut écrire })
.
Pour la seconde question, la majoration, valable à partir de
est 
.
Pour la seconde question, la majoration, valable à partir de
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :