Convergence absolue d'une série

par **Ewok** » 12 Nov 2007, 00:22

Bonsoir!
J'ai une suite (un) à valeurs complexes telle que le module de chacun de ses termes soit inférieur stric à 1 et telle que la série des |un| converge.
Je veux montrer que la série des ln|1+un| est absolument convergente, mais j'arrive seulement à montrer qu'elle est convergente... Il faudrait simplement que j'arrive à montrer que |ln|1+un|| est inférieur à ln(1+|un|) mais...ça bloque^^ Si vous pouviez m'aider...merci d'avance!

par **Isomorphisme** » 12 Nov 2007, 01:05

Bonsoir,

Tu peux utiliser l'inégalité triangulaire :

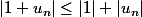
et le tour est joué.

par **Ewok** » 12 Nov 2007, 01:11

Euh...je me retrouve avec ln|1+un| (et non pas |ln|1+un||) inférieur à ln(1+|un|), non?

par **rifly01** » 12 Nov 2007, 01:42

Salut,

Je pense que tu dois remarquer ceci :

De cette inégalité tu peux dire :

car |u_n|>0.

Ce qui te permet de conclure à la convergence de

.

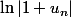
par **Ewok** » 12 Nov 2007, 01:57

Mais ça me permet pas d'en déduire que

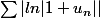
converge...non?
Ce que j'aimerai faire c'est montrer que

pour en déduire du théorème sur les séries à termes équivalents positifs que

converge donc

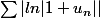
converge...

par **Ewok** » 12 Nov 2007, 22:44

Si je peux me permettre de relancer ce sujet :lol2:

par **bitonio** » 12 Nov 2007, 22:52

Si

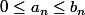
et

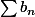
converge, alors

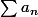
converge.

par **Ewok** » 12 Nov 2007, 22:55

Ah d'accord merci!
Edit: Euh en fait non...J'ai bien:

mais pas

ou bien j'ai rien compris?^^

par **bitonio** » 12 Nov 2007, 22:56

bitonio a écrit:

Faux d'ailleurs ^^

par **Ewok** » 12 Nov 2007, 23:00

bitonio a écrit:J'ai édité

Moi de même...Désolée d'avoir autant de mal :triste:

par **bitonio** » 12 Nov 2007, 23:01

Pas grave, on est tous passé par là ^^ (et encore moi j'en suis pas sorti :triste: !)

par **Ewok** » 12 Nov 2007, 23:03

bitonio a écrit:Pas grave, on est tous passé par là ^^ (et encore moi j'en suis pas sorti :triste: !)

Si t'avais lu mon édition tu verrais que j'ai toujours pas percuté le truc :ptdr:
Tu la montres comment l'inégalité avec la valeur absolue?

par **bitonio** » 12 Nov 2007, 23:15

Il semble en effet que je sois passé à la valeur absolue comme un barbare, ce qui n'est bien sûr pas autorisé (et sûrement pas vérifié!). Je réfléchis...

par **yos** » 12 Nov 2007, 23:39

En plus de la majoration de

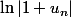
par

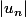
, tu peux obtenir une minoration :

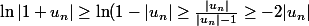
La dernière inégalité pour

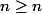
0 puisque la suite tend vers 0.
Finalement

.
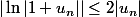
A améliorer.

par **tize** » 12 Nov 2007, 23:41

Ewok a écrit:... montrer que |ln|1+un|| est inférieur à ln(1+|un|)

C'est vrai ça ?
sinon tu peux montrer que

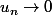
et pour

proche de 0, on :

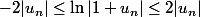
par **Ewok** » 13 Nov 2007, 00:00

Excuse moi mais j'ai pas compris comment tu procèdes pour les trois dernières étapes de ta minoration...

PS: Sinon tize je sais pas du tout si "c'est vrai ça" mais ça m'aurait arrangé^^

par **yos** » 13 Nov 2007, 00:11

Tize et moi arrivons à la même chose.

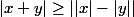
(bien connu et facile).

facile avec

.
Tu peux aussi court-circuiter l'avant-dernière étape en montrant que

pour x entre 0 et 1/2.
...

par **Ewok** » 13 Nov 2007, 00:21

Ok merci beaucoup à vous tous!

Convergence absolue d'une série

Convergence absolue d'une série

Qui est en ligne