Merci pour vos réponses.
Si pour simplifier, on suppose que

admet un unique point de discontinuité
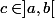
, alors, on de manière évidente que

est continue sur
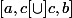
(elle y est même dérivable).
Mais
quid de la continuité en

?
En fait, si je pose cette question, c'est à cause de la preuve suivante :
Je cherche à montrer que l'indice d'un point

par rapport à un lacet

, défini par
 = \frac{1}{2 i \pi} \int_{\gamma}{\frac{dz}{z-a}})
est un entier.
(On appelle lacet une application
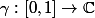
de classe

par morceaux et telle que
=\gamma(1))
et on suppose que
)
.)
Pour cela, on note

l'ensemble (fini) des points de

où

n'est pas

et on définit la fonction
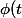=\exp\left(\int_{0}^{t}{\frac{\gamma'(s)}{\gamma(s)-a}}\right))
.
On a alors, pour

,
}{\phi(t)} = \frac{\gamma'(t)}{\gamma(t) - a})
et donc, après calcul, la fonction

définie par
=\frac{\phi(t)}{\gamma(t)-a})
est de dérivée nulle sur
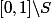
, donc constante sur
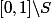
et, par suite, constante sur

.
C'est ce dernier passage que je ne comprends pas...
Si l'on savait que

était continue sur

tout entier, on pourrait conclure. Mais là, on n'a a priori la continuité que sur
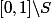
...
Imaginons par exemple que
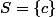
avec
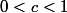
.
Pourquoi ne peut-on pas avoir
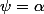
(constante) sur
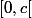
et
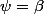
(autre constante) sur
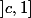
? Pourquoi a-t-on nécessairement
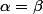
et
=\alpha)
?