Limite et DL d'une fonction définie par une intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 03 Juin 2014, 17:38
Bonjour,
l'exercice suivant me donne du fil à retordre :
On pose
=e^{1/x} \displaystyle\int_0^x e^{-1/t} \mathrm{d}t)
.
1. Limité en
de
)
.
2. Développement limité à l'odre
en
de
.
Déjà pour la première question je galère, j'ai essayé des changements de variables, une IPP, des majorations... rien n'y fait
Merci de me mettre sur la voie :we:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 03 Juin 2014, 18:20
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 03 Juin 2014, 18:25
Impec merci beaucoup !
Pour la question 2, une petite indication ? :happy2:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 03 Juin 2014, 19:26
Hello,
Tu peux faire des intégrations par parties successives je pense.
Ça doit pouvoir aboutir.
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 03 Juin 2014, 21:08
J'ai essayé comme ça :
=e^{1/x} \int_0^x e^{-1/t} \mathrm{d}t = e^{1/x} \int_0^x t^2(\dfrac{1}{t^2}e^{-1/t}) \mathrm{d}t)
)
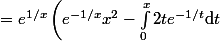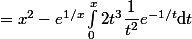
et on peut continuer en refaisant le même type d'intégration par parties dans la nouvelle intégrale.
Est-ce à ça que tu pensais ?
Mais comment trouver le DL à l'ordre
quelconque ? :hein:
Par ailleurs je ne sais même pas si on a
)
...
-
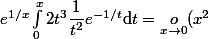Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
par Robic » 03 Juin 2014, 21:24
Pour trouver le développement limité à l'ordre quelconque, on pourrait calculer les coefficients du développement, donc les dérivées successives en 0.
Ou alors on calcule le développement limité de la dérivée de phi puis on l'intègre ? Mais il y a une fonction devant l'intégrale, ça va compliquer...
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 03 Juin 2014, 21:32
Robic a écrit:Pour trouver le développement limité à l'ordre quelconque, on pourrait calculer les coefficients du développement, donc les dérivées successives en 0.
Ou alors on calcule le développement limité de la dérivée de phi puis on l'intègre ? Mais il y a une fonction devant l'intégrale, ça va compliquer...
J'y ai pensé mais les dérivées successives ne semblent pas simples à obtenir.
Le développement limité de
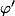
ne me paraît pas vraiment plus simple à avoir que celui de
, puisqu'on a
=-\dfrac{1}{x^2} \varphi(x) +1)
:spy:
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
par Robic » 03 Juin 2014, 22:15
C'est vrai que cet exercice a l'air bien compliqué...
Normalement, dans ce genre de question, on n'a pas à calculer l'intégrale (ça se trouve elle est incalculable), il faut plutôt utiliser les méthodes dont je parlais, mais en effet ça ne mène pas à grand chose on dirait...
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 04 Juin 2014, 00:53
ça semble effectivement assez coton...
Perso, comme
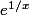
tend vers
(super vite) et
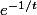
vers 0 (super vite aussi...) j'essayerais de les "mélanger" pour voir ce qu'il reste :
=\int_0^xe^{1/x-1/t}dt\)
puis, en faisant le changement de variable
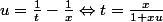
=\int_\infty^0e^{-u}\frac{-x^2 du}{(1+xu)^2}=x^2\int_0^\infty\frac{e^{-u}}{(1+xu)^2}du)
Sauf erreur, vu sous cette forme, on montre facilement que
est de classe
et que son D.L. commence par
.
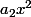
Tu peut alors utiliser ta formule
=-\frac{1}{x^2}\varphi(x)+1)
pour trouver les coeffs du D.L. de proche en proche.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
