Continuité d'une fonction définie par une intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 16 Juil 2021, 11:17
par Romanouch » 16 Juil 2021, 11:17
Bonjour,
Pour a et b deux réels avec a<b, la fonction
F définie sur

par
=\int_{a}^{b} e^{xt}dt)
est-elle continue sur

?
Je pense que non (problème en x=0) mais en lisant ce cours (
http://exo7.emath.fr/cours/ch_intpar.pdf) et en appliquant le théorème 1 de continuité de la page 1, j'ai l'impression de pouvoir prouver qu'elle est continue et ça me perturbe.
Où est mon erreur svp?
Bonne journée.
-
Vassillia
 par Vassillia » 16 Juil 2021, 13:32
par Vassillia » 16 Juil 2021, 13:32
Bonjour,
Tu as raison pour le théorème.
Ce qui te dérange, je présume c'est que
=\frac{e^{xb}-e^{xa}}{x})
si
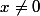
La limite est indéterminée lorsque

tend vers 0, pour lever l'indétermination, tu peux essayer de faire un développement limité si tu connais cette notion.
Modifié en dernier par Vassillia le 16 Juil 2021, 14:22, modifié 1 fois.
-
Lunns
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Juil 2021, 08:53
-
 par Lunns » 16 Juil 2021, 13:58
par Lunns » 16 Juil 2021, 13:58
Bonjour,
Pourquoi ne pas utiliser le théorème de continuité des intégrales à paramètres ?
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 16 Juil 2021, 14:03
par Romanouch » 16 Juil 2021, 14:03
}{x}=b-a+o(1))
Donc la limite de F(x) quand x tend vers 0 vaut b-a, qui est aussi la valeur pour F(0). Donc F est prolongeable par continuité en 0.
C'est bien ça?
-
Vassillia
 par Vassillia » 16 Juil 2021, 14:06
par Vassillia » 16 Juil 2021, 14:06
Oui mais même pas besoin de prolonger car par définition :
=\frac{e^{xb}-e^{xa}}{x})
si
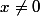
et
=\int_a^b 1dt=b-a)
si

.
Tu viens de démontrer la continuité de

, le théorème dont tu parlais permet de le faire sans avoir besoin d'étudier les limites. Je t'ai proposé cette méthode pour que tu réalises que ce n'est pas contradictoire.
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 17 Juil 2021, 14:22
par Romanouch » 17 Juil 2021, 14:22
J'ai compris.
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
