Convergence d'une fonction définie par une intégrale.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 11 Mar 2006, 15:28
par Anonyme » 11 Mar 2006, 15:28
Bonjour, je coince sur le problème suivant.
On me demande :
si a et b sont 2 réels vérifiant aI=intégrale de a à b de f(x).sin(nx) dx (pour n appartenant à N) converge vers 0.
Bon on me dit d'intégrer par parties, donc je pose u=f(x) et v'=sin(nx)
et je trouve :
I=(1/n)[-f(b)cos(nb) + f(a)cos(na) + intégrale de a à b de f'(x).cos(nx)dx]
et puis ?
Merci de votre aide.
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 11 Mar 2006, 15:51
par El_Gato » 11 Mar 2006, 15:51
Salut,
Eh bien ca y'est tu as fini la preuve: majore les cosinus par 1 et f' dans l'intégrale par son sup sur [a,b]. C'est le 1/n que tu as mis en premier qui conduit tout çà vers 0:
Considérons
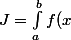 e^{inx}\mbox{d}x)
, pour faire plus simple.
On a :
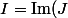)
et
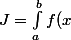\mbox{d} \[ \frac{1}{in}e^{inx}\])
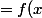\frac{1}{in} e^{inx}\]_a^b - \frac{1}{in} \int_a^b e^{inx} f'(x) \mbox{d} x)
.
Donc
 \frac{1}{n}M_2)
où
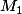
et
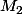
sont respectivements les Sup de f et de sa dérivée sur [a,b], sup qui existent puisque f est supposée de classe

sur [a,b].
Donc:
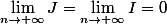
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités