Congruence et élément inverse

[Beta]

Bonjour,

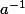
On définie un élément inverse pour un certain modulo comme étant .

Ainsi, je me posais la question suivante : comment trouver cet inverse dans tout les cas, car pour le moment je procède de manière assez intuitive pour des petites valeurs mais que faire pour quand ce n'est pas évident, pour des grandes non réductible à de plus petit valeurs par exemple.

Merci de votre intérêt envers ce message

Bonne journée
Beta

[Mimosa]

Bonjour

Ca ne marche pas dans tous les cas. Par exemple, 2 n'a pas d'inverse modulo 6, mais 5 en a bien un (lequel?)

Tu verras plus tard que si n est un nombre premier tous les entiers non multiples de n ont un inverse. Il existe même des algorithmes pour les calculer. Tu peux te faire une idée en regardant "théorème de Bézout" et "algorithme d'Euclide".

[Beta]

Bonjour Mimosa,

Merci pour votre réponse. Je crois que j'ai finalement compris.
Comme l'inverse est possible ssi alors on trouve u et v des entiers tel que par Bézout
Or, donc
Donc

Merci beaucoup !

Beta

[Mimosa]

Bravo! C'est exactement ça.