Combinatoire

[jlb]

Bonjour, j'aimerai savoir comment lorsqu'on lance 3dés (ou plus) déterminer le nombre de façon d'obtenir une somme donnée pour la somme des faces de ces dés.
Avec un petit programme, j'arrive à trouver cela facilement. Peut-on déterminer cela par des calculs pas trop compliqués? Merci.

[zygomatique]

salut

soit s = a + b + c la somme des faces des trois dés avec a, b et c entiers compris entre 1 et 6.

il y a 6^3 issues ... et tout le problème est de compter le nombre d'issues correspondant à la somme s.

les somme varient donc de 3 à 18 ....

dans le cas de 3 dés et après avoir fait un tableau pour deux dés ....

j'en ai déduit 6 tableaux pour les 6 valeurs du troisième dé ... puis compter (fait par le logiciel) ...

sinon P(a + b + c = k) = P(b + c) = k - i / a = i) (probabilité conditionnelle) ....

[Lostounet]

Salut jlb!
Tu as probablement cherché mais regarde ici un moyen joli et visuel pour la somme de deux dés avec des dominos:

Source:
http://villemin.gerard.free.fr/Wwwgvmm/ ... htm#tot2de

Et puis un petit tableau pour le 3ème comme propose Zygomatique, pourquoi pas une pyramide en 3D? Ou quelque chose comme ça
Je regarde.

[Ben314]

Salut,
En utilisant la notion de Série génératrice, on montre facilement que, si on note le nombre de façon d'obtenir une somme de en jetant dés à 6 faces alors :
et pour tout entier relatif non nul .
Puis, pour tout entier naturel non nul on a :
pour tout 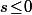et pour tout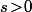

Ce qui te permet de calculer les valeur à l'aide d'un simple tableur, soit en créant 6 colonnes "fictives" pour s=-1,-2,...,-6, soit en mettant des formules différentes dans les colonnes s=1,2,...6 de celles dans les colonnes s>7.

Il y aurais évidement d'autres formules plus ou moins explicite pour déterminer les , la plus évidente de toutes étant évidement
.

[Robot]

Qu'est-ce que tu appelles "façon d'obtenir" ? Est-ce que (4,5) et (5,4) sont deux façons différentes d'obtenir un total de 9 ? Le résultat dépend de façon cruciale de ta réponse à cette question.

[jlb]

Merci à vous pour vos remarques et aides! Bonne fin de journée .

[zygomatique]

soit

alors le coefficient de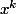 dans le développement de te donne le cardinal de l'événement (s = k) (pour un lancer de deux dés)

pour n dés on élève P à la puissance n ....

bon courage ....

[Robot]

Tu pourrais au moins répondre à ma question.

[zygomatique]

Tu pourrais au moins répondre à ma question.

il me semble que tu te trompes d'interlocuteur ....

j'ai donné une méthode pratique (à l'aide d'un tableur) ... puis une formule générale .... à l'aide des séries génératrices ....


EDIT : ou alors tu t'adresses à JLB ....

[Robot]

Il ne me semble pas t'avoir posé de question.
Mais on ne sait toujours pas ce que jlb appelle "façon d'obtenir".

[jlb]

Bonsoir Robot, désolé de ne t'avoir répondu: je ne suis pas le chevalier de Méré!! L'interprétation de Lostounet, Zygo et Ben était ce que j'attendais: à l'exercice classique avec deux dés pour connaître la loi de la somme, je me suis demandé ce qu'il en était pour plusieurs dés et au final, un petit programme semble le plus simple. Je ne suis pas très doué et si tu as des infos supplémentaires, je suis preneur par curiosité ( ensemble {}au lieu de n upplet (...)) Merci en tout cas à tous pour votre participation.

[Robot]

OK. L'autre problème de dénombrement est plus coton.

[beagle]

Pour 3 dés on pourrait avoir une formule du genre
pour faire un total de k; nombre de cas possibles =
C( 2 , k-1 ) - 3(k-8)(k-7)/2

j'ai pas le temps de vérifier plus.
k plus petit que 8 la soustraction n'existe pas, on ne rajoute pas (je me méfie avec vous!)

[beagle]

ok beagle , je vérifie pour k=3
C( 2 , 3-1) = C(2,2) =1
c'est avoir 1et1et1, un seul cas.
marche plutôt bien beagle, bravo!
peu importe si les autres sont faux...

[beagle]

je suis désolé beagle, non cela ne marche pas au-delà de 14,
déjà pour 15 faut rajouter 3 je pense,
l
il faudrait un petit raccord pour 15,16,17,18
mais j'ai pas le temps

[beagle]

Bon pas le temps de vérifier si c'est bon déjà au niveau calcul, si on tpmbe bien sur le résultat attendu,
ensuite au-delà de 15, possible que l'on doive rajouter 3 (1) , 3(1+2), and so on
maintenant si c'est symétrique, si axe de symétrie entre 10 et 11, faut pas se crever pour rajouter un patch pour le au-delà de 15
La formule donnée a le mérite de donner idem pour k=10 (36-9=27) et k=11 (45-18 =27)
les symétriques 8 et 13
k=8 (21-0= 21), k=13 (66-45=21)

PS au-dela de 14 il faut rajouter ce qui est enlevé en trop
si c'est pour 15: 3(1), pour 16: 3(1+2), pour 17 :3(1+2+3)
alors pour 18 : 3(1+2+3+4)= 30
pour 18 la formule devenant
C(2,17) = 130 on enlève 3(18-8)(18-7)/2 =165, et on rajoute le trop enlevé 30
136-165+30= 1
donc doit y avoir du bon quand même la-dedans.

[chan79]

Salut
Juste pour le fun
Avec 6 dés, en exprimant la fréquence de chaque somme, ça a un petit air de Gauss




salut beagle, je vais regarder ce que tu as mis

[beagle]

Bonjour mon Chan79.
Un fil combinatoire et toujours pas de Chan79, je te croyais en vacances ou malade!
Bon alors le début c'est comme tu me l'avais montré un jour, c'est un grand classique,
je prends k éléments sur une ligne et bing je coupe au ciseau ou bien je rajoute les éléments de séparation,
ici ben on coupe dans les intervalles.
Bref cela donne le C(2, k-1).
Le soucis c'est que l'on va avoir des dés de plus de 6.Il faut virer ces éléments là.
Alors je n'étais pas parti pour trouver une idée générale, mais j'ai commencé à jouer avec un seul dé sup à 6 à éliminer.D'où la première formule.
Au départ j'avais bien en tète que c'était insuffisant mais comme je fais des petits bouts de réflexion entre deux trucs au boulot, j'ai zappé et me suis emballé.
Néanmoins la manière de compter les plus de 6, ben en fait on peut ratrapper le fait qu'on les compte en trop, d'où mon rajout final qui peut se systématiser.
Au final une formule pas très belle que l'on doit pouvoir améliorer.
Mais cohérente.Le but initial du fil 3 dés je veux sans les énumérer un par un ètre capable de calculer combien de possibiltés pour un k donné.Presque fait, non?

[beagle]

Pour Gauss, cela concentre à la moyenne, c'est pas surprenant quand même.

[beagle]

n'empèche que lorsqu'on se dit que c'est symétrique,
trouver le 6 + 6 +6 un seul cas
en faisant l'opération:136-165+30= 1
c'est très inesthétique.
Fallait pas prendre ce combat là.
Bon c'était pour voir la cohérence et la systémisation possible...