en effet je me suis embrouiller
donc pour b(n) je trouve
b(n)=a(n)+a(n-1)+......+1(suite arithmetique)
pour la serie formelle de b(n) je n'arrive pas a simplifié le resultat(en appliquant le resultat precedent
Combinatoire serie generatrice
23 messages
- Page 2 sur 2 - 1, 2
par girdav » 06 Avr 2010, 14:50
On peut encore arranger l'expression de )
car on connaît les )
et ça nous ramène à une somme classique.
par Ben314 » 06 Avr 2010, 16:52
A mon avis (donc c'est pas complètement évident...), l'idée de l'exercice c'est de ne pas chercher à calculer explicitement les 
(ni les termes correspondant au nombre de soluces dans le cas général) dans un premier temps, mais d'obtenir quand même les fonctions générétrices par du "calcul formel".
Par exemple, vu queX^n=\frac{1}{(1-X)^2})
, que =1=a(0))
et que pour
, = a(n) +b(n-1))
, on a :
\ =\ \sum_{n\geq 0}b(n)X^n\ <br />=\ b(0)+\sum_{n\geq 1}\big(a(n)+b(n-1)\big)X^n\ <br />=\ a(0)+\sum_{n\geq 1}a(n)X^n+\sum_{n\geq 1}b(n-1)X^n)
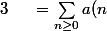X^n+X^2\sum_{n\geq 0}b(n)X^n\ <br />=\ \frac{1}{(1-X)^2}+X g(X))
Ce qui donne)
sans calculs suplémentaires (et se généralise "les doigts dans le nez" aux cas suivants...)
Par exemple, vu que
Ce qui donne
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
23 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :