Rayon de convergence d'une série génératrice

[Thouny71]

Bonjour à tous,

Je suis actuellement en train de faire un exercice de proba en utilisant les séries génératrices.
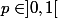
Je dois calculer le rayon de convergence qui est ci dessous avec et q=(1-p).



J'ai donc sorti le un et voulant utiliser après du théorème de dérivation terme à terme d'une série entière mais je n'arrive pas à aboutir.

Merci de votre aide

[tournesol]

c'est la dérivée d'une série géométrique de raison pt , donc même rayon de convergence que la série primitive .