Fonction génératrice des moments (loi exponentielle)

[Shaddan]

Bonjour, j'avais comme exercice de calculer la fonction génératrice des moments de la loi exponentielle, et je pense y être arrivé avec le calcul ci-dessous, mais il y a en fait une étape que je fais simplement parce-que je sais à quel résultat je dois arriver et sans vraiment comprendre le comment du pourquoi, donc si quelqu'un pouvait m'expliquer, ça m'aiderait bien.
Voici le calcul que j'ai fait :

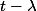
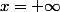
et mon problème est que je ne comprends pas pourquoi à la 3ème ligne serait forcément négatif. Si il était positif, le résultat divergerait quand , j'en ai donc conclu que c'était négatif et donc que ça convergeait vers , mais je n'arrive pas à comprendre pourquoi.

Merci d'avance pour vos explications.

[arnaud32]

ta fonction n'existe effectivement pas sur R tout entier mais sur
generalement tu vas t'en servir au voisinage de 0 pour trouver les moments.

[Shaddan]

Merci pour la réponse.
En fait ce que je ne comprends pas c'est que la loi exponentielle étant

et la définition de la fonction génératrice de moments

l'intégrale que j'ai au départ me parait correcte, à moins que je me sois trompé quelque part.
Donc comment faudrait-il faire ressortir la condition ?
Faudrait-il écrire quelque chose du genre

ou y a-t-il une raison différente pour laquelle serait inférieur à ?

[arnaud32]

ton integrale du depart n'existe pas si t est superieur ou egale a lambda, elle diverge.
donc tu definis juste ta fonction sur un sous ensemble de R

[Shaddan]

Désolé pour la réponse tardive.
D'accord, donc en fait il faut tout simplement de définir l'intégrale sur un sous-ensemble de .
Merci pour ton aide.