Changement de base matrice

[sarah79]

Bonjour,
j'ai un souci avec le théorème de changement de base.
Voici l'énoncé :
Soit f appartenant à L|K(E) où E es un espace vectoriel de dimension finie. On se donne deux bases B et C de E. Soit P la matrice(inversible) des coordonnées dans la base B des éléments de C. Alors:

MatB(f)=P*MatC(f)*P(-1)

je ne comprends pas la logique comment on peut savoir que ce n'est pas :
MatC(f)=P*MatB(f)*P(-1)

Pouvez vous m'expliquer ou me donner une démonstration svp?
P va de la base C vers B ou ça n'a rien a voir?

[AlexisD]

Bonjour,

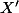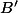Visiblement, ce qui te dérange, c'est la cohérance de la formule. Néammoins, si tu as bien compris que pour tout , en notant [resp ], la matrice de dans une base [resp ] et 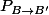la matrice de passage de à 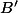, alors:



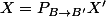
C'est ainsi qu'on en déduit la relation de changement de base pour un endomorphisme quelconque.

Mais je suis d'accord que devant de telles formules, on puisse se mélanger les pinceaux. Il est bon d'avoir un truc mnémotechnique pour les retenir. Je te confie la mienne.

En notan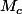t et 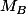les matrices de f dans les bases C et B, la formule dit:

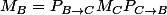
avec



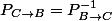
En fait je m'arrange pour avoir la lettre C au centre, et ca parait plus clair.

C'est une technique qui vaut ce qu'elle vaut, mais elle m'a sortit de plusieurs situations !

[Ben314]

Il y a des tas de moyen mnémotechnique de retrouver la formule.
Comme je suis une grosse bille, je refait quasi la preuve à chaque fois...
Si les vecteurs de la base C sont U1:(1 2 3) , U2:(4 5 6) , U3:(7 8 9) exprimé dans la base B [il faut les écrire en colonne mais j'ai la flemme] alors la matrice de passage P de B à C est :
1 4 7
2 5 8
3 6 9
Si tu applique ta matrice à un vecteur (x y z) [en colonne] tu obtient le vecteur (X Y Z) = x.(1 2 3)+y.(4 5 6)+z.(7 8 9) [toujours en colonne ou c'est nettement plus visuel]
Et là, tout s'éclaire, on est en train de calculer V=x.U1+y.U2+z.U3 et de chercher les coordonnées de ce vecteur dans la base B (vu qu'on a pris les coordonnées de U1, U2 et U3 dans la base B). Bien évidement, (x y z) [en colonne], vu que V=x.U1+y.U2+z.U3, c'est les coordonnées de V dans la base C.
Résumé : la matrice P, elle donne les coordonnées dans la base B connaissant celle dans la base C (en fait elle porte pas trés bien son nom)
et, évidement, P^-1 donne les coordonnées dans C connaissant celle dans B.

Conclusion :
- Si dans un calcul cohérent tu as M.P où M est une matrice, M doit être la matrice d'un endomorphisme dans la base B vu que le résultat de P.quelque_chose, c'est des coordonnées dans la base B.
- Si dans un calcul cohérent tu as P.N où N est une matrice, N doit être la matrice d'un endomorphisme dans la base C vu que, quand on applique P à quelque chose, le quelque chose ça doit être des coordonnées dans la base C.
Evidement, c'est le contraire avec P^(-1)

Edit : Grillé par AlexisD qui semble avoir une méthode mnémotechnique "pas con" (perso, j'ai juste le "elle porte mal son nom" et je me démerde, mais faut que je réfléchisse à chaque fois...)

[sarah79]

Bonjour,

Visiblement, ce qui te dérange, c'est la cohérance de la formule. Néammoins, si tu as bien compris que pour tout , en notant [resp ], la matrice de dans une base [resp ] et la matrice de passage de à , alors:



C'est ainsi qu'on en déduit la relation de changement de base pour un endomorphisme quelconque.

Mais je suis d'accord que devant de telles formules, on puisse se mélanger les pinceaux. Il est bon d'avoir un truc mnémotechnique pour les retenir. Je te confie la mienne.

En notant et les matrices de f dans les bases C et B, la formule dit:

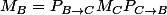
avec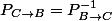



En fait je m'arrange pour avoir la lettre C au centre, et ca parait plus clair.

C'est une technique qui vaut ce qu'elle vaut, mais elle m'a sortit de plusieurs situations !

j'ai un souci quand meme P(B->C) = matrice des élements de B dans la base C?

[sarah79]

MatB(f)=P*MatC(f)*P(-1)

P d'après mon théorème est la matrice des éléments de C dans la base B donc P(C->B) et donc :

matB(f)=P(C->B)*matC(f)*P(B->C) ce qui ne colle pas??

[AlexisD]

Regarde mieux. Ton tout premier message est juste. Ce que tu viens d'écrire est en revanche erroné...

[sarah79]

Je ne comprends pas c'est vous qui avez mal lu mon message ou alors je ne comprends vraiment rien.

[Ben314]

MatB(f)=P*MatC(f)*P(-1) CORRECT

P d'après mon théorème est la matrice des éléments de C dans la base B donc P(C->B) NON et donc :

matB(f)=P(C->B)*matC(f)*P(B->C) NON PLUS ce qui ne colle pas??

Je t'ai déja démontré dans le post juste au dessus que la matrice des coordonnées des éléments de C dans la base B [appelée "matrice de passage de B à C"] elle permet de calculer les coordonnées dans B connaissant celle dans C, c'est à dire que, si X=PX', cela signifie que le même vecteur à pour coordonnées X dans B et X' dans C.

Reregarde le post d'AlexisD, cette matrice est celle qu'il note P(B->C)

[AlexisD]

MatB(f)=P*MatC(f)*P(-1)

P d'après mon théorème est la matrice des éléments de C dans la base B donc P(C->B) et donc :

matB(f)=P(C->B)*matC(f)*P(B->C) ce qui ne colle pas??

Non justement. On écrit les coordonnées des vecteurs de C dans la base B. Donc on passe de la base B à la base C. C'est bien la matrice de passage de B vers C.

Ceci pour te convaincre, j'espère: la matrice de passage P(B->C) est la matrice de l'application identité de E muni de la base C dans E muni de la base B.

[sarah79]

d'accord merci beaucoup pour toutes vos explications.