Matrice et changement de base

par **juliette92** » 03 Mai 2010, 15:24

Bonjour, j'ai besoin d'aide pour l'exercice suivant notamment pour le b).

Dans l'espace vectoriel réel ([R^4, +,.), soient P le plan vectoriel d'équation :
x-2y+3z+t=0
x+y-z+4t=0
et Q le plan vectoriel engendré par u = (1,1,1,1) et v = (-1,2,0,3).

a) Montrer que P et Q sont supplémentaire dans R^4.
b) Ecrire la matrice de la symétrie s par rapport à P et direction Q dans la base canonique de R^4.

Merci d'avance.

par **Arnaud-29-31** » 03 Mai 2010, 15:30

Bonjour,

Ou est-ce que tu bloques ?

Qu'as tu à ta disposition pour montrer que

?

On a une base de Q, ca serait pas mal de trouver une base de P ...
Ca donne quoi ?

par **juliette92** » 03 Mai 2010, 18:23

En fait pour la question (a) c'est bon, je bloque plutot pour la (b)..

par **Arnaud-29-31** » 03 Mai 2010, 18:28

Et bien as-tu trouvé une base de P ?

par **juliette92** » 03 Mai 2010, 20:03

oui j'ai trouver la famille ( w=(-1/3 , 4/3 , 1 , 0),x=(-3 , -1 , 1 , 0) )

pour la (b) si je traduit la symétrie par rapport à P de direction Q,
s(u)=-u
s(v)=-v
s(w)=w
s(x)=x

et j'ai écrit la matrice S' de s dans la base ( u v w x ) et là je ne sais pas comment faire ..

par **Arnaud-29-31** » 03 Mai 2010, 20:14

On a la matrice de s dans la base (u,v,w,x)

On la veux dans

.

Il faut peut-être exprimer la matrice passage de la base canonique

à la base (u,v,w,x).

Avant de faire ça, je glisse juste une petit remarque : ton vecteur x ne me convient pas des masses ... Mais je suppose que c'est une simple erreur de frappe, vu que le vecteur (-3,-1,0,1) convient.

par **juliette92** » 03 Mai 2010, 20:51

Oui c'est une faute de frappe. je ne sais pas comment faire pour exprimer la matrice de passage...

par **Arnaud-29-31** » 03 Mai 2010, 20:57

Ah ...

Tu as bien trouvé tes vecteurs u,v,w,x tels que :

Donc P, matrice de passage de

à (u,v,w,x) = ??

par **juliette92** » 03 Mai 2010, 21:17

Euuuh P=
1 -1 -1/3 -3
1 2 4/3 -1
1 0 1 0
1 3 0 1

??

par **Arnaud-29-31** » 03 Mai 2010, 21:20

Affirm !

On a donc maintenant la matrice de s dans (u,v,w,x), la matrice de passage de la base canonique à la base (u,v,w,x).

Il ne reste plus qu'a appliquer la formule de changement de base pour exprimer la matrice de s dans la base canonique.

par **juliette92** » 03 Mai 2010, 21:22

c'est bien la formule S = PS'P^-1 ..?
Mais alors il faut calculer aussi l'inverse de P =O

par **Arnaud-29-31** » 03 Mai 2010, 21:25

C'est ça oui ...

Et oui il faut

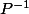
:mur: , enfin si on a la flemme, on peut peut-être demander à super TI de nous faire ça :p

par **juliette92** » 03 Mai 2010, 21:31

lol d'accord alors je devrais y arriver pour la fin !
merci beaucoup, bonne soirée :)

par **Arnaud-29-31** » 03 Mai 2010, 21:32

De rien, bonne soirée à toi aussi :)

Matrice et changement de base

Matrice et changement de base

Qui est en ligne