Centre de symétrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Déc 2018, 10:55
par mehdi-128 » 27 Déc 2018, 10:55
Bonjour,
On se place dans un repère orthonormé. Soit
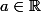
La fonction
)
a un graphe qui se déduit de celui de

par symétrie par rapport à la droite d'équation
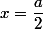
(j'ai fait la démo sans souci)
Montrer en utilisant le résultat ci-dessus que si la fonction

vérifie
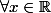
:
=-f(x))
alors le graphe de

admet
)
comme centre de symétrie.
Je ne vois pas comment procéder.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 27 Déc 2018, 11:05
par pascal16 » 27 Déc 2018, 11:05
tu pars d'une vision géométrique du fait qu'un point M(x,y) ait pour image M'(x',y') par symétrie centrale de centre (a/2;0).
puis M est un point de la courbe représentative de f implique que ses coordonnées sont du type (x;f(x)).
Il faut que son image M' soit aussi sur la courbe
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 27 Déc 2018, 11:09
par FLBP » 27 Déc 2018, 11:09
Salut,
Une façon de faire est de montrer que pour
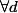
:
 dt = 0)
Un changement de variable est c'est fait ...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Déc 2018, 11:20
par mehdi-128 » 27 Déc 2018, 11:20
FLBP trop compliqué pour moi.
Pascal je sais plus comment trouver les coordonnées d'un point image d'une symétrie qui n'est pas de centre l'origine du repère...
Puis je vois pas où utiliser que f(a-x)=-f(x)
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 27 Déc 2018, 11:29
par FLBP » 27 Déc 2018, 11:29
Comme je disais c'est un simple changement de variable :
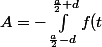 dt = \int_{\frac{a}{2}-d}^{\frac{a}{2}+d} f(a-t) dt)
si
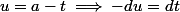
:
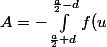 du = \int_{\frac{a}{2}-d}^{\frac{a}{2}+d} f(u) du)
En changeant juste la lettre

en

:
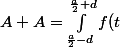 dt -\int_{\frac{a}{2}-d}^{\frac{a}{2}+d} f(t) dt = 0 \implies A = 0)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Déc 2018, 19:14
par mehdi-128 » 27 Déc 2018, 19:14
Pourquoi la solution d'Aviateur a disparu alors qu'elle était intéressante ?

J'ai pas eu le temps de l'étudier ce matin.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Déc 2018, 19:21
par mehdi-128 » 27 Déc 2018, 19:21
pascal16 a écrit:tu pars d'une vision géométrique du fait qu'un point M(x,y) ait pour image M'(x',y') par symétrie centrale de centre (a/2;0).
puis M est un point de la courbe représentative de f implique que ses coordonnées sont du type (x;f(x)).
Il faut que son image M' soit aussi sur la courbe
Pascal je comprends votre raisonnement mais vous partez de la conclusion donc vous faites la contraposée.
Je ne comprends pas du coup : il faut montrer que si
=-f(x)) alors
alors (a/2,0) est centre de symétrie du graphe de f.
J'ai réussi avec votre méthode mais ça montre la contraposée du coup je sais pas comment faire

-
aviateur
 par aviateur » 27 Déc 2018, 19:36
par aviateur » 27 Déc 2018, 19:36
Voilà.
Soit M=(x,f(x)) appartenant au graphe G.
Son symétrique M'=(x',y') par rapport à A=(a/2,0) vérifie
(x+x')/2=a/2, (f(x)+y')/2=0. C'est à dire que x'=a-x et y'=-f(x).
Mais f('x)=f(a-x)=-f(x)=y', ce qui veut dire M' appartient à G.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 03:01
par mehdi-128 » 28 Déc 2018, 03:01
J'ai compris tout le raisonnement sauf la fin pourquoi le fait que f(x')=y' implique que M' appartienne à G ?
Si

est définie sur

il faudrait montrer que
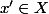
?

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 28 Déc 2018, 10:02
par nix64 » 28 Déc 2018, 10:02
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 10:22
par mehdi-128 » 28 Déc 2018, 10:22
Belle preuve mais j'ai des choses qui me bloquent.
Si j'ai la fonction
)
alors
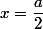
est axe de symétrie de

Mais ici quelle est la fonction ? J'ai juste une relation :
=-f(x))
Du coup comment savez-vous que
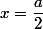
est axe de symétrie de

alors qu'on sait pas qui est f et qu'on a juste une relation ?
Aussi comment montrez vous que
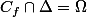
est un centre de symetrie pour

?
-
aviateur
 par aviateur » 28 Déc 2018, 10:39
par aviateur » 28 Déc 2018, 10:39
mehdi-128 a écrit:J'ai compris tout le raisonnement sauf la fin pourquoi le fait que f(x')=y' implique que M' appartienne à G ?
Si

est définie sur

il faudrait montrer que
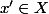
?
@Medhi est ce qu'un jour tu vas faire un vrai effort pour réfléchir?
Tu donnes une fonction définie sur R alors X=R !!!!!!!
Evidemment quand on se pose ce genre de question, il faut que a/2 soit au centre de X. Si ce n'était pas le cas on ne se la poserait même pas la question. Mais de plus X=R!!!!
Il va falloir un jour que tu commences à te poser les vraies bonnes questions et non pas des questions saugrenues.

-
nix64
- Membre Relatif
- Messages: 109
- Enregistré le: 06 Déc 2018, 10:17
-
 par nix64 » 28 Déc 2018, 10:58
par nix64 » 28 Déc 2018, 10:58
tu as raison rien ne garantie que

est un axe de symétrie pour

ni pour
)
on a juste

et
)
sont symétriques par rapport à

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 11:13
par mehdi-128 » 28 Déc 2018, 11:13
@Aviateur
L'énoncé est bizarre aussi :
si
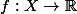
vérifie
=-f(x))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 11:18
par mehdi-128 » 28 Déc 2018, 11:18
@Nix
D'accord mais vous n'avez pas montré que :
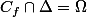
est un centre de symetrie pour

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 11:29
par mehdi-128 » 28 Déc 2018, 11:29
Mais vous avez raison ça ne sert à rien de vérifier que x' est dans X vu que c'est un centre de symétrie de la courbe donc forcément il est au centre de X.
J'appliquais bêtement la définition du graphe d'une fonction qui dit que c'est l'ensemble des (x,f(x)) où x appartient à X qui est le domaine de définition de f.
-
aviateur
 par aviateur » 28 Déc 2018, 11:45
par aviateur » 28 Déc 2018, 11:45
Oui c'est ça. Mais essaye de voir les choses a priori.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 28 Déc 2018, 12:35
par mehdi-128 » 28 Déc 2018, 12:35
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités

est un axe de symetrie pour


est un centre de symetrie pour

et y = 0 car y= f(a/2)=-f(a/2)
est définie sur
il faudrait montrer que
?