Caractérisation de la borne supérieure
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ihsen
- Membre Naturel
- Messages: 13
- Enregistré le: 29 Juin 2017, 09:42
-
 par Ihsen » 16 Nov 2017, 12:02
par Ihsen » 16 Nov 2017, 12:02
Bonjour à vous tous.
Voici l'énoncé de l'exercice :
On considère une partie A de R non vide et bornée.On définit l'ensemble des distances entre éléments de A :
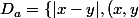\in A^{2} \right\})
.
On me demande de montrer que
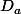
possède une borne supérieur notée
=supD_{a})
ensuite de montrer que :
=supA-infA)
.
Déja je tiens a connaître la différence entre
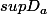
et
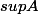
Merci pour votre aide !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Nov 2017, 12:33
par chan79 » 16 Nov 2017, 12:33
salut
Avec

=]1;3[
la borne supérieure de

est 3.
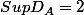

-
vejitoblue
- Membre Relatif
- Messages: 133
- Enregistré le: 21 Nov 2017, 11:27
-
 par vejitoblue » 26 Nov 2017, 01:33
par vejitoblue » 26 Nov 2017, 01:33
A no vide donc contient un x, donc Da contient |x-x|
A borné donc il existe M>0 tq |x|<=M pour tout x dans A
|x-y|<|x|+|y|<=2M donc Da est borné
Da est borné non vide donc admet une borne sup delta
mais la borne sup de Da c'est la plus grande distance possible entre deux élément de A

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Nov 2017, 09:00
par chan79 » 26 Nov 2017, 09:00
Soit un élément de Da, distance entre deux nombres x et y de A, avec x>=y
x<=supA
y>=infA
-y<=-infA
on a x-y<=supA-infA
soit |x-y|<=supA-infA
supA-infA est un majorant de Da
Ensuite:
soit

>0
il existe x et y de Da avec x>=y tels que
supA-x <=

et
x-infA<=

(supA-infA)-(x-y)<=

+

=

démonstration à détailler
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités