Propriété de la borne supérieure
15 messages
- Page 1 sur 1
Propriété de la borne supérieure
Bonsoir,
j'ai la propriété suivante :
Toute partie non vide majorée de IR possède une borne supérieure.
Bon, bah le problème est que ca me semble évident car si il y a un majorant, alors il y a une borne sup. Mais pourquoi cette propriété est réputée comme "difficile" à démontrer ?
Je suis sûr de faire une erreur de raisonnement....
D'ailleurs quelle est pour vous la meilleur définition de IR ?
Merci d'avance
j'ai la propriété suivante :
Toute partie non vide majorée de IR possède une borne supérieure.
Bon, bah le problème est que ca me semble évident car si il y a un majorant, alors il y a une borne sup. Mais pourquoi cette propriété est réputée comme "difficile" à démontrer ?
Je suis sûr de faire une erreur de raisonnement....
D'ailleurs quelle est pour vous la meilleur définition de IR ?
Merci d'avance
Bonsoir,
ce n'est pas que c'est difficile à démontrer, c'est que ça ne se démontre pas, c'est un axiome appelé axiome de la borne supérieure.
Une définition de R ? Justement, R est à un isomorphisme près l'unique corps totalement ordonné vérifiant la propriété de la borne supérieure :lol3:
Edit : Il est d'ailleurs interressant, bien que difficile, de montrer qu'un corps totalement ordonné vérifiant l'ABS est isomorphe à R.
ce n'est pas que c'est difficile à démontrer, c'est que ça ne se démontre pas, c'est un axiome appelé axiome de la borne supérieure.
Une définition de R ? Justement, R est à un isomorphisme près l'unique corps totalement ordonné vérifiant la propriété de la borne supérieure :lol3:
Edit : Il est d'ailleurs interressant, bien que difficile, de montrer qu'un corps totalement ordonné vérifiant l'ABS est isomorphe à R.
bjr,
 peut être construit de manière que toute suite de Cauchy ait une limite.
peut être construit de manière que toute suite de Cauchy ait une limite.
Soit A une partie non vide majorée. l'ensemble B de ses majorants est une partie non vide minorée.
On choisit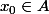 et
et 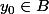 . Ensuite on regarde si
. Ensuite on regarde si 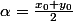 est élément de A ou de B. Par dichotomie (et récurrence) , on construit deux suites adjacentes et de Cauchy
est élément de A ou de B. Par dichotomie (et récurrence) , on construit deux suites adjacentes et de Cauchy 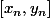 , telles que:
, telles que:
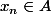
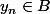
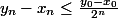
On obtient alors:
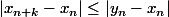
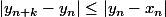
Les deux suites sont de Cauchy et convergent vers la même limite l.
On montre ensuite que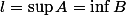
Soit A une partie non vide majorée. l'ensemble B de ses majorants est une partie non vide minorée.
On choisit
On obtient alors:
Les deux suites sont de Cauchy et convergent vers la même limite l.
On montre ensuite que
Merci de vos réponses
busard_des_roseaux >
tu as démontré qu'il existait toujours une suite de cauchy qui convergeait vers la borne sup de ton ensemble.
A est une partie de IR, non ?
Pourquoi avoir montré ca avec une suite necessaurement de cauchy ? on pourrait le démontrer plus simplement avec une suite quelconque, non ?
En fait ce que tu veux me montrer ca ne serait pas que justement quelquesoit l'ensemble qu'on prend puisque qu'il existe une suite de cauchy qui atteint sa borne sup, on peut construire chaque réel avec une limite de suite de cauchy ?
En tout cas je ne vois pas pourquoi on a besoin que la suite soit de cauchy ?
merci d'avance
busard_des_roseaux >
tu as démontré qu'il existait toujours une suite de cauchy qui convergeait vers la borne sup de ton ensemble.
A est une partie de IR, non ?
Pourquoi avoir montré ca avec une suite necessaurement de cauchy ? on pourrait le démontrer plus simplement avec une suite quelconque, non ?
En fait ce que tu veux me montrer ca ne serait pas que justement quelquesoit l'ensemble qu'on prend puisque qu'il existe une suite de cauchy qui atteint sa borne sup, on peut construire chaque réel avec une limite de suite de cauchy ?
En tout cas je ne vois pas pourquoi on a besoin que la suite soit de cauchy ?
merci d'avance
Salut,
tout dépend de ta définition de IR, mais de toute façon il me semble qu'il y a équivalence entre IR est complet et IR possède la propriété de la borne supérieure.
Si par exemple, tu pars de la contruction de IR avec les suites de Cauchy,
alors tu montres d'abord le critère de Cauchy (ie IR est complet) et ensuite tu l'utilises pour montrer la propriété de la borne supérieure.
tout dépend de ta définition de IR, mais de toute façon il me semble qu'il y a équivalence entre IR est complet et IR possède la propriété de la borne supérieure.
Si par exemple, tu pars de la contruction de IR avec les suites de Cauchy,
alors tu montres d'abord le critère de Cauchy (ie IR est complet) et ensuite tu l'utilises pour montrer la propriété de la borne supérieure.
ffpower a écrit:ah ok..c vrai qu on pourrait en fait faire un peu nimp sinon^^.mais le theoreme qu enonce nightmare me semble pas tres dur alors(a moins que j ai p-e passé outre certaines difficultés,ce qui est bien possible)
Jord avait déjà donné un lien sur cette question sur ce forum: http://www.ilemaths.net/forum-sujet-171459.html , (qui ne marche plus apparemment), ça s'appelle le théorème d'Eudoxe.
lapras a écrit:En tout cas je ne vois pas pourquoi on a besoin que la suite soit de cauchy ?
juste pour être sûr que ces suites ont une limite (auquel cas cette limite
est la borne sup dont on souhaite démontrer l'existence). Au fait, on dit "supremum" et "infimum" maintenant au lieu de borne sup et borne inf ?
je vois les choses comme ça:
1) on peut construire
2) on construit
3) Tous les ensembles
ou à isomorphisme unique près, je crois que ça fait une grosse différence.
Bonsoir,
Justement c'est faux, si je prends par exemple comme ensemble l'ensemble des idéaux de Z ordonnés par l'inclusion (ou Z lui-même ordonné par la relation de divisibilité), toute partie est majorée mais il n'y a pas forcément de borne sup : par exemple la partie {6Z} est majorée par les idéaux 2Z, 3Z et Z, on ne peut pas choisir une borne sup entre 2Z et 3Z car ils ne sont pas comparables pour la relation d'ordre choisie.
lapras a écrit:si il y a un majorant, alors il y a une borne sup.
Justement c'est faux, si je prends par exemple comme ensemble l'ensemble des idéaux de Z ordonnés par l'inclusion (ou Z lui-même ordonné par la relation de divisibilité), toute partie est majorée mais il n'y a pas forcément de borne sup : par exemple la partie {6Z} est majorée par les idéaux 2Z, 3Z et Z, on ne peut pas choisir une borne sup entre 2Z et 3Z car ils ne sont pas comparables pour la relation d'ordre choisie.
Bonjour,
j'ai une démonstration: A non vide majoré dans R => Sup(A) existe dans R, qui utilise la propriété des segments emboîtés de R.
Je me demandais si c'était équivalent à partir avec les suites de Cauchy comme l'a fait busard_des_roseaux.
Voici une esquisse de ma démo:
---
On choisit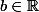 qui majore
qui majore  et
et 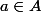 . On pose
. On pose 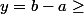 et
et 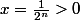 . Comme
. Comme  est Archimédien, il existe
est Archimédien, il existe 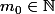 tel que
tel que 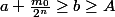 .
.
Une fois qu'on a ça, on pose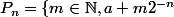 majore
majore  qui est non vide et possède un plus petit élément (dans
qui est non vide et possède un plus petit élément (dans  ) qu'on peut noter
) qu'on peut noter  .
.
Ensuite on pose2^{-n}, a+p_n 2^{-n}]) .
.
On montre que et
et  s'interceptent, que
s'interceptent, que ) est croissante au sens des ensembles et finalement sous l'hypothèse de
est croissante au sens des ensembles et finalement sous l'hypothèse de  que
que 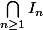 est réduit à un point
est réduit à un point  .
.
Enfin on montre que est un majorant puis le plus petit des majorants de
est un majorant puis le plus petit des majorants de  ce qui finit la démonstration (assez longue quand elle est détaillée).
ce qui finit la démonstration (assez longue quand elle est détaillée).
---
On utilise partout le fait que est Archimédien, je voulais savoir s'il y a une implication (sans doute) avec la complétude ou un équivalence. Quelles sont les propriétés les plus "historiques" ?
est Archimédien, je voulais savoir s'il y a une implication (sans doute) avec la complétude ou un équivalence. Quelles sont les propriétés les plus "historiques" ?
j'ai une démonstration: A non vide majoré dans R => Sup(A) existe dans R, qui utilise la propriété des segments emboîtés de R.
Je me demandais si c'était équivalent à partir avec les suites de Cauchy comme l'a fait busard_des_roseaux.
Voici une esquisse de ma démo:
---
On choisit
Une fois qu'on a ça, on pose
Ensuite on pose
On montre que
Enfin on montre que
---
On utilise partout le fait que
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
