Exercices de la borne supérieure?!!

[Anonyme]

bonjour à tous
voila un exercice qui me pérturbe déjà
A et B deux parties non vides et borné de R.
C={abs(a-b);a apparient a A , b de B}
1)montrer que supC existe
2)monter que abs(supA-supB)=
une autre question de cours qui m'enerve:
pouquoi on dit que :
pour que X admette une borne sup, il est evidemment necessaire que X soit majoré.cette condition n'est pas suffisante en générale. ????
je ne comprends plus rien

merci d'avance de votre aide

[Chimerade]

[quote="Non inscrit"]bonjour à tous
voila un exercice qui me pérturbe déjà
A et B deux parties non vides et borné de R.
C={abs(a-b);a apparient a A , b de B}
1)montrer que supC existe
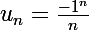
2)monter que abs(supA-supB)=0) défini par . Cet ensemble est majoré par 1/2 et tous les nombres supérieurs. Et il ne possède pas de borne supérieure !

[Anonyme]

Pkoi {Un,n€IN*} n' admettrait pas de borne sup ?

[khivapia]

Je crois que dans l'exemple c'est 1/2 la borne supérieure ?!? vu qu'il majore l'ensemble des Un et qu'en plus il est dedans, c'est même plus qu'une borne sup, c'est le plus grand élément.

Le fait que la condition soit suffisante est une des propriétés dues à la construction de R : pour R, on a "Toute partie non vide majorée admet une borne supérieure" ce qui n'est pas vrai pour Q.

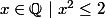
Par exemple admet dans R la borne sup mais n'a pas de borne sup dans Q !

[Chimerade]

Je crois que dans l'exemple c'est 1/2 la borne supérieure ?!? vu qu'il majore l'ensemble des Un et qu'en plus il est dedans, c'est même plus qu'une borne sup, c'est le plus grand élément.

Le fait que la condition soit suffisante est une des propriétés dues à la construction de R : pour R, on a "Toute partie non vide majorée admet une borne supérieure" ce qui n'est pas vrai pour Q.

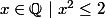
Par exemple admet dans R la borne sup mais n'a pas de borne sup dans Q !

OOps ! Désolé ! Je crois que j'ai confondu les définitions...
Merci Khivapia de l'avoir signalé.
Pour me rattraper, je proposerai alors dans Q :
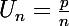
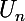
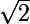
avec Là les auraient une borne supérieure s'ils étaient défini dans R (qui est ) mais n'en ont pas dans Q.
Mes excuses à "non inscrit"