Calcul de distance d'un centre vers un hexagone

[chandlerb67]

Bonjour

Voici mon problème du jour,
Soit un repère orthonormé avec un point (x,y).
Ce point représente le centre d'un hexagone Est-Ouest


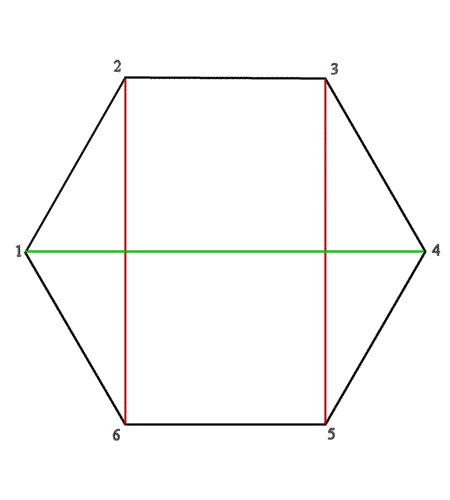
Je voudrais pouvoir construire l'hexagone de centre (x,y) qui passe par le point (x',y').
La difficulté est de déterminer à l'avance sur quel segment se trouve ce point.

A la base mon mon objectif est de connaitre le rayon de l'hexagone de centre (x,y), passant par (y,y').
Or la distance entre les 2 points ne permet pas (à priori) de présumer de ce rayon car sur un axe de l'hexagone de rayon, chaque point possède une distance différente du centre.
Pensez-vous qu'une formule est possible ou doit-on passer par un algorithme ?

Merci de votre aide.
Chandler

[Dlzlogic]

Bonjour,
Si j'ai bien compris, vous connaissez le centre (x,y) de l'hexagone tel que dessiné sur la figure, donc vous connaissez les 6 directions de ses sommets.
Vous avez un point (x', y') et vous cherchez le rayon de l'hexagone qui passe par le point.
Vous pouvez dessiner le côté de l'hexagone qui passe par ce point, donc, vous connaissez toute la figure, donc, vous pouvez en calculer tous les éléments.

[chandlerb67]

Bonjour,
Si j'ai bien compris, vous connaissez le centre (x,y) de l'hexagone tel que dessiné sur la figure, donc vous connaissez les 6 directions de ses sommets.
Vous avez un point (x', y') et vous cherchez le rayon de l'hexagone qui passe par le point.
Vous pouvez dessiner le côté de l'hexagone qui passe par ce point, donc, vous connaissez toute la figure, donc, vous pouvez en calculer tous les éléments.

Merci de ta réponse mais ce qui te parait simple ne l'est pas pour moi :we:
Si je savais dessiner l'hexagone, je saurai le rayon et si je savais trouver le rayon je pourrais le dessiner. Si je pose la question c'est que je n'arrive ni à l'un, ni à l'autre.

En supposant que x'>x et y'<y je ne sais pas déterminer si (y,y') est sur le segment {2,3} ou sur le segment {3,4}. Evidemment si il est sur le segment {2,3} le rayon est y-y'. Sur le segment {3,4} le calcul du rayon ne me saute pas aux yeux.

Merci

[chandlerb67]

Afin d'être plus précis et de simplifier l'hexagone est régulier comme sur l'illustration

[Dlzlogic]

Afin d'être plus précis et de simplifier l'hexagone est régulier comme sur l'illustration

Bon, alors je vais être plus précis. Il y a donc 3 droites (6 demi-droites) qui passent par le contre et qui font un angle de 60° entre-elles.
On peut facilement tracer les 3 bissectrices. La droite passant par le point (x', y') et perpendiculaire à la bissectrice concernée est le support du côté concerné.
Le dessin de la figure permet sans difficulté de définir les relations métriques entre les éléments de la figure.

[fatal_error]

salut,

La difficulté est de déterminer à l'avance sur quel segment se trouve ce point.

Si on nomme O le centre du cercle et M_0 le point sur l'axe des abscisses à droite, et M le point que tu sais pas à quel coté il appartient, il suffit de trouver l'angle formé par les vecteurs et

pour ca un coup de produit vectoriel:

cad

avec le vecteur unitaire correspondant au vecteur
si on on note
on a
ensuite, il te reste plus qu'à trouver k tel que

[Dlzlogic]

Bonjour Faral_error,
En fait, on ne sait pas très bien dans quel contexte ce problème est posé, c'est pour ça que je n'ai pas été plus précis dans ma réponse.
La disposition de l'hexagone tel que sur la figure n'est pas une simplification, mais fait partie intégrante de l'énoncé, sinon, le problème n'est pas défini.

"La difficulté est de déterminer à l'avance sur quel segment se trouve ce point."
Je n'ai pas vraiment compris cette phrase. Les probabilistes répondront 1 chance sur 6, moi, je dis que c'est pas à l'avance, il n'y a pas plusieurs choix et la méthode qui consiste à le construire à la main est une bonne méthode pour trouver la formulation mathématique.

[fatal_error]

salut,

ca me parait pourtant clair.
On a le centre de lhexagone O(x,y).
On a un point quelconque M(x',y'), et on veut déterminer le rayon du cercle dans lequel est inscrit l'hexagone, tel que le point M est sur l'un des côtés de l'hexagone.

La question de chandler67, c'est : donnés O et M, sur quel côté de l'hexagone se trouve M.

[Dlzlogic]

salut,

ca me parait pourtant clair.
On a le centre de lhexagone O(x,y).
On a un point quelconque M(x',y'), et on veut déterminer le rayon du cercle dans lequel est inscrit l'hexagone, tel que le point M est sur l'un des côtés de l'hexagone.

La question de chandler67, c'est : donnés O et M, sur quel côté de l'hexagone se trouve M.

Oh, mais naturellement, j'ai bien compris le problème.
Ce que je n'ai pas compris c'est ce qui fait dire à Chandeler "la difficulté est de déterminer à l'avance .."
Dans quel contexte se trouve-t-il ? que cherche-t-il à calculer ? s'agit-il d'un exercice ? pourquoi à l'avance ? serait-ce avant de connaitre le point M ? etc.

Tu oublies un point fondamental de l'énoncé, et qui n'est pas "pour simplifier", c'est que l'on connait la direction des axes de symétrie de l'hexagone. Sinon, il y a une infinité de solutions comprises entre L et L sqrt(3)/2, si L est la distance entre O et M.

[fatal_error]

la formule n'est pas possible parce que larcsin prend ses valeurs dans l'intervalle qui correspond à [-pi/2;pi/2] autrement dit pour toute la partie [pi/2, 3pi/2] il faut procéder à la symétrie pi - angleTrouve.

sinon voilà un petit script, ca déboite pas, mais c'est marrant :we:

Code: Tout sélectionner





body{
   margin:0;
   padding:0;
}
#canvas{
  background-color:#eeeeee;
}


function toY(y){
  return -y+400;//400=canvas.height
}
function clearPlot(ctx, param){
  ctx.clearRect ( 0 , 0 , 400 , 400 );
}
function plotPolygone(ctx,param){
   var C=param.C,
         n=param.n,
         rho=param.rho;
  ctx.beginPath();
  ctx.moveTo(C[0]+rho, toY(C[1]));
  for(var i=0;i=C[0] && M[1]










[Dlzlogic]

Ah, oui, j'aime bien.
Y'a très longtemps que j'ai pas fait du JavaScript, moi, c'est plutôt C/C++ et PHP.

[chandlerb67]

salut,

ca me parait pourtant clair.
On a le centre de lhexagone O(x,y).
On a un point quelconque M(x',y'), et on veut déterminer le rayon du cercle dans lequel est inscrit l'hexagone, tel que le point M est sur l'un des côtés de l'hexagone.

La question de chandler67, c'est : donnés O et M, sur quel côté de l'hexagone se trouve M.

Oui c'est exactement cela.
Ta formulation est pourtant simple, mais cela fait presque 20 ans que je n'ai pas fait de maths et j'ai eu de mal à le mettre en équation.
Ton code m'a bien aidé aussi.

Merci de tes réponses, j'ai trouvé mon bonheur.