Borne sup, borne inf

[chombier]

Bonsoir,

Je m'arrache les cheveux sur un problème sans doute assez simple...

On a deux sous ensemble A et B de tel que



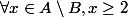
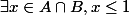
Il s'agit simplement de prouver que inf A >= inf B

Par moment ça me parait évident mais difficile à montrer formellement.
Par moment je ne suis même plus sur que ce soit vrai.

Merci d'avance de m'éclairer !

[mathelot]

bonsoir,
...................

[chombier]

Merci mathelot, et désolé : j'ai fait une erreur sur la deuxième assertion. Il fallait lire :

On a deux sous ensemble A et B de tel que



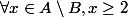
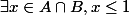
J'ai corrigé mon premier message

[Ben314]

Salut,

On a deux sous ensemble A et B de tel que
(1)
(2)

C'est "concon" ton truc :
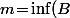Si on pose , alors le point (2) nous dit que .
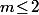
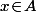
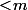
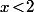
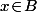
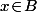
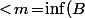S'il existait un qui soit alors on aurait et on aurait forcément (sinon un tel contredirait le point (1)) sauf qu'un qui soit , ben ça peut pas exister...
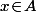
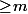
Donc tout les sont et ça prouve que .

[chombier]

Je crois que j'ai trop simplifié mon problème et qu'il a perdu de sa substance. Je recommence donc, en esperant que cela modélise bien ma situation (qui est dans cadre d'espaces métriques et de distances, mais cela n'a pas d'intérêt ici) :

Soient A et B deux ensemble inclus dans un même ensemble E et f une fonction de E dans .

On a :
(1)
(2)

Il faut cette fois montrer que

Merci d'avance pour votre patience et votre compréhension !

[Ben314]

Il faut cette fois montrer que

Ben c'est exactement la même chose qu'avant vu que ce qu'on note régulièrement , ben par définition même, c'est .

[chombier]

Merci beaucoup Ben.

Parfois il est difficile de voir si on s'évertue à prouver des évidences et s'il est nécessaire de rentrer dans ce niveau de détail (sachant qu'il faut tout de même en être capable).

Pas toujours facile de trouver le juste milieu.

[Pseuda]

Bonsoir,

Je m'arrache les cheveux sur un problème sans doute assez simple...

On a deux sous ensemble A et B de tel que



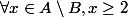
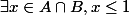
Il s'agit simplement de prouver que inf A >= inf B

Bonsoir,

Ou bien (un peu tard), par l'absurde. Si .
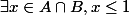
De : , on en tire :
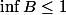
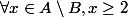
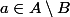
De : , on aboutit à une contradiction, car et .

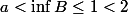
[chombier]

On a deux sous ensemble A et B de tel que



Il s'agit simplement de prouver que inf A >= inf B

J'ai trouvé une preuve sans absurde ni contraposée (grâce à vous !!) :




,

[chombier]

Propriétés utilisées :
1) :


2) :



Je crois que j'ai fait le tour. Encore merci à vous !!

Si j'ai dit des betises, tapez moi dessus

[Pseuda]

J'ai trouvé une preuve sans absurde ni contraposée (grâce à vous !!) :

Bonsoir,

A la 2ème ligne, tu veux dire : .

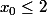
[Pseuda]

2) :

C'est le contraire :

(il n'y a pas le marteau dans les smileys, je n'ai pas pu appliquer la consigne )

[chombier]

Merci Pseuda ! J'ai corrigé pour la posterité !