Bijection de R2 dans R

[alex26]

Bonjour,

Savez vous s'il existe une bijection de R² dans R et si oui en avez vous un exemple ?

D'avance merci
Alex

[sky-mars]

f ( p ,@ ) = p cos @
p € ] o , +OO [
et @ € ] 0 , pi [ est une bijection de R² dans R par exemple

[alex26]

Nickel, merci :-)

[sky-mars]

^^ ;) de rien

[Jonny]

Salut,
Désolé mais je comprends pas un truc

f ( 1 , Arcos(1/2) ) = 1/2

f ( 2 , Arccos(1/4) ) = 1/2

C'est donc pas bijectif ? :hum:

De la même manière, la valeur @=pi/2 n'est pas exclue, donc comment définir l'image de 0 par la réciproque de f ?

[Nightmare]

Salut :happy3:

Tous les hyperespaces ont la puissance du continue (c'est à dire que pour tout n, . ) En terme bijectif, tous les hyperespaces sont équipotent à .

Par contre, ils ne sont pas isomorphes pour des raisons de dimension.

[emdro]

f ( p ,@ ) = p cos @
p € ] o , +OO [
et @ € ] 0 , pi [ est une bijection de R² dans R par exemple

Bonsoir,

je ne comprends pas...

1) f :] o , +OO [x ] 0 , pi [ ->IR et non de IR²->IR

2) f(racine(2), pi/4)=f(2, pi/3). f n'est pas injective.

[alex26]

Je retire mes remerciements en fait. J'ai lu trop vite. Ce n'est évidemment pas une bijection. Est une bijection R² dans R² : (p cos(@), p sin(@))

[alex26]

Salut :happy3:

Tous les hyperespaces ont la puissance du continue (c'est à dire que pour tout n, . ) En terme bijectif, tous les hyperespaces sont équipotent à .

Par contre, ils ne sont pas isomorphes pour des raisons de dimension.

C'est absurde ce que tu dis car deux ensembles sont équipotents s'il existe une bijection de l'un sur l'autre. Et l'argument des dimensions ne tient pas car R n'est pas dénombrable...

[Jonny]

C'est absurde ce que tu dis car deux ensembles sont équipotents s'il existe une bijection de l'un sur l'autre. Et l'argument des dimensions ne tient pas car R n'est pas dénombrable...

Je pense qu'il parle de R^n en temps que R espace vectoriel.

Et il me semble avoir vu en cours que card(R)=card(R^n) pour tout n.
Ca a un nom du genre Aleph 1. C'est de mémoire, m'en tenez pas rigueur ^^

[sky-mars]

oula !

Autant pour moi !
:hum: :hum: :hum: :hum: :marteau: :cry:

[Nightmare]

C'est absurde ce que tu dis car deux ensembles sont équipotents s'il existe une bijection de l'un sur l'autre. Et l'argument des dimensions ne tient pas car R n'est pas dénombrable...

Qu'est-ce qui est absurde? Tous les sont équipotents c'est bien ce que je dis?

Concernant les dimensions, comme le souligne jonny je sous-entendais en tant qu'espace vectoriel sur ou .

[Nightmare]

Bref, pour répondre à la suite de la question, les bijections sont pas faciles à trouver.

Cantor a démontré qu'il existait une bijection de [0,1] dans le carré [0,1]², on la compose avec une bijection de [0,1]² dans R² connue.

Je ne crois pas qu'on sache exprimer de bijection de [0,1] dans [0,1]² cela dit.

[kazeriahm]

Il faut aussi noter qu'il n'existe pas de bijection continue de R^2 dans R, car R^2 privé d'un point est toujours connexe par arcs, ce qui n'est jamais le cas de R privé d'un point

[Nightmare]

Effectivement. Est-ce qu'il existe une surjection continue? :lol3:

[alex26]

Qu'est-ce qui est absurde? Tous les sont équipotents c'est bien ce que je dis?

Concernant les dimensions, comme le souligne jonny je sous-entendais en tant qu'espace vectoriel sur ou .

Oui, ce que tu dis est absurde car contradictoire. Relis toi : tu dis d'abord que 3$\rm \mathbb{R}^{n} est équipotent à 3$\rm \mathbb{R}, ce qui laisse entendre qu'il existe une bijection entre 3$\rm \mathbb{R}^{n} et 3$\rm \mathbb{R} puis tu dis qu'ils ne sont pas isomorphes, ce qui maintenant laisse entendre qu'il n'existe pas de bijection entre les deux ensembles... ou peut-être t'es tu mal exprimé ?

[alex26]

Bref, pour répondre à la suite de la question, les bijections sont pas faciles à trouver.

Cantor a démontré qu'il existait une bijection de [0,1] dans le carré [0,1]², on la compose avec une bijection de [0,1]² dans R² connue.

Je ne crois pas qu'on sache exprimer de bijection de [0,1] dans [0,1]² cela dit.

Encore une fois ça ne marche pas car Cantor a effectivement démontré l'existence d'une telle bijection et on peut explicitement la donner mais la bijection est entre N² et N. R étant indénombrable on ne peut pas étendre ce résultat à R.
Si tu as d'autres idées je suis preneur... mais peut-être que ça n'existe pas en fait

[Nightmare]

Euh, isomorphes équipotents !

Ce que j'ai dit est juste et cohérent. Les espaces ne sont pas isomorphes mais bien équipotents.

Pour la bijection entre [0,1] et le carré je suis formel, Cantor a prouvé son existence ...

[busard_des_roseaux]

bonjour alex26,


j'explicite ce qu'a écrit NightMare:

Il y a une bijection entre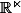 et , c'est à dire qu'il y a autant de points sur un segment [0;1] ou
sur une droite que dans l'espace tout entier.

Par contre, il n'y a pas de bijection bicontinue ( et continue) entre et 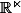, (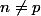) car ces espaces ne se comportent pas de la même façon quand on les troue en leur ôtant une boule fermée ou qu'on les partitionne en deux (on évoque le groupe fondamental 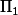de classes d'homotopie de lacets)

[yos]

Dans le même ordre d'idée, il y a l'exo d'oral :

il y a pas de surjection de classe de [0,1] dans .

Ca me semble clair à cause des coins du carré : l'arc doit y passer tout en gardant le dos rond. De là à le rédiger proprement, il faudrait que je réfléchisse. Si vous avez des idées...