Bijection dans N
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 17:00
par lomdefer » 07 Oct 2006, 17:00
Dsl j'avais pas vu, oui ok soit f(1)=0 ou f(1)=1, mais la definition de la bijectivité c'est que pour tout

il existe un unique

tel que
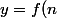)
.Donc on peut pas avoir les deux.
Mais lequel on choisi ??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 17:03
par tize » 07 Oct 2006, 17:03
lomdefer a écrit:Dsl j'avais pas vu, oui ok soit f(1)=0 ou f(1)=1, mais la definition de la bijectivité c'est que pour tout

il existe un unique

tel que
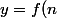)
.Donc on peut pas avoir les deux.
Mais lequel on choisi ??
Exactemtent et comme 0 est déjà pris par f(0)=0 on a nécessairement f(1)=...
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 17:08
par lomdefer » 07 Oct 2006, 17:08
f(1)=1 bien sur !!
Suis-je bête !
Eu on a donc comme hypathèse de récurrence :
:="S_n=f(n)=n")
C'est ça ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 17:14
par tize » 07 Oct 2006, 17:14
T'as tout compris, tu peux continuer tout seul je pense... :++:
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 17:19
par lomdefer » 07 Oct 2006, 17:19
Donc par recurrnce je montre que P_n est vraie et cela voudra dire que :

n|--->n
Donc
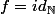
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 17:25
par lomdefer » 07 Oct 2006, 17:25
une dernière question.
Une fois que j'ai montrer que P_n est vraie pour tout n appartient à N différent de 0.
Donc il ya combien de bijection de N dans N ?
n-1 c'est ça ?
vu que pour 0 sa marche pas...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 17:32
par tize » 07 Oct 2006, 17:32
lomdefer a écrit:une dernière question.
Une fois que j'ai montrer que P_n est vraie pour tout n appartient à N différent de 0.
Donc il ya combien de bijection de N dans N ?
n-1 c'est ça ?
vu que pour 0 sa marche pas...
QUOI ?!!!
Je pense que finalement tu n'as pas du tout compris... :briques:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 07 Oct 2006, 17:32
par Zebulon » 07 Oct 2006, 17:32
Bonjour,
vous avez montré que si f était une bijection de

telle que pour tout n,
\leq{n})
, alors
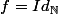
. Réciproquement,

est bien sûr une bijection de

vérifiant
\leq{n})
quel que soit n. Il y a donc une et une seule bijection de

vérifiant cette condition!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
