Bijection de N dans N

[Anonyme]

Bonjour, est-il vrai que toute bijection s de N dans N vérifie s(n) équivalent à n en + l'infini ?

[girdav]

Bonjour,
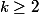
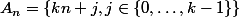
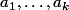
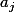
on fixe un entier . On pose . Si on note dans l'ordre les éléments de , on applique à tous les la permutation qui à renvoie . On a alors, en notant la permutations sur ainsi obtenue que et dès lors on voit que l'on ne peut avoir .

[Anonyme]

Merci mais je ne comprends pas la conclusion ? Le terme tend bien vers un non ?

[girdav]

Ah oui exact, donc le "contre-exemple" est bidon.

[girdav]

Je retente un truc, sur mon brouillon ça a l'air de marcher, mais si je faisais le compte de tous les trucs qui marchent sur mon brouillon mais pas en vrai...).
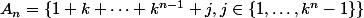
On pose tout en gardant le reste de mon premier message.
On a

[Ben314]

Salut,
Un contre exemple simple consiste à considérer la fonction qui envoie les nombres pairs sur les puissances de deux.
Plus précisément, l'image du n-ième nombre pair est la n-ième puissance de 2 et l'image du n-ième nombre impair est le n-ième entier qui n'est pas puissance de 2.

[Anonyme]

Merci à vous deux !

[girdav]

Il fallait penser à des permutations un peu tordues, suffisamment pour que l'on n'ait pas mais pas trop pour que l'on puisse les trouver !

[Nightmare]

Salut !

Le résultat me semble vrai si l'on remplace N à l'arrivé et au départ par N* !

[girdav]

Salut !

Le résultat me semble vrai si l'on remplace N à l'arrivé et au départ par N* !

Comment le montres-tu?

[Nightmare]

Je ne sais pas, en fait, je crois bien que j'ai dit n'importe quoi.

Par contre, si on sait d'avance que s(n)/n converge, ça ne peut être que vers 1.

[Ben314]

Salut !

Le résultat me semble vrai si l'on remplace N à l'arrivé et au départ par N* !

Je vois pas trop ce que ça change : je prend comme image du n-ième nombre pair non nul la n-ième puissance de 2 (qui elle est forcémént non nulle) et, comme image du n-ième nombre impair (don non nul !!!) le n-ième entier non nul et non puissance de 2
En bref :
2->1 ; 4->2 ; 6->4 ; 8->8 ; 10->16 ; ... ; 2n->2^(n-1)
1->3 ; 3->5 ; 5->6 ; 7->7 ; 9->9 ; 11->10 ; 13->11 ; 15->12 ; ... ;
(on peut surement donner la forme explicite de f(2n+1) mais ça ne sert à rien...)

[mathelot]

Tiens, une petite conjecture

il n'y a pas de s telle que ?

[lapras]

Comme l'a dit Nightmare si s(n)/n converge c'est vers 1 donc si s(n) eq. l(n), s(n)/n tend vers 0 impossible.