Bonsoir,
Je viens de commencer l'arithmétique (et je n'en ai pas fais en TS : j'étais en physique) et je n'arriva à rien avec cet exo. Donc si vous pouviez m'aider à le résoudre, ce serait formidable. Merci d'avance pour votre aide.
1.
Valuation p-adique de 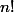
Soient
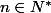
, et
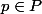
. On se propose de déterminer la puissance de

figurant dans la décomposition en facteurs premiers de

.
On note
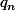
le plus grand entier

tel que
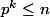
.
(a) Montrer que pour tout
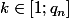
, le nombre de multiples (au sens large) de
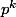
inférieurs ou égaux à

est
)
.
(b) Calculer, selon la valeur de
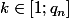
, le nombre de multiples de
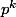
exactement inférieurs ou égaux à

.
(c) Ecrire alors la valeur de la puissance de

recherchée faisant intervenir une somme, puis après simplification, en déduire que cette puissance est :
 + E(\frac{n}{p^2}) + ... + E(\frac{n}{p^{q_n}}))
