Arithmétique dans Z
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 18 Jan 2007, 18:52
par pouik » 18 Jan 2007, 18:52
Bonsoir,
Dans votre message ne s'agit-il pas plutot en fait de
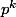
et de

à la place de ce qui est souligné ?
fahr451 a écrit:on fait la somme de tous les exposants de p présents dans n!
il y a E(n/p) -E(n/p^2) nbres qui ont 1 comme puissance de p
il y a E(n/p^2) -E(n/p^3) nbrs qui 2 ..........
il y a E(n/p^k) E(n/p^(k+1) nbrs qui ont k ....... ( k fixé )
d'où un exposant total ds n! égal à
1[(E(n/p)-E(n/p^2) ] + 2 (E(n/p^2)-E(n/p^3)] +...+q(n)E(n/p^(q(n))
égal à
E(n/p)+E(n/p^2) +... +E(n/p^(q(n))par simplification
Merci d'avance pour votre réponse
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Jan 2007, 19:00
par fahr451 » 18 Jan 2007, 19:00
ben non on cherche la puissance de p dans n!
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 18 Jan 2007, 19:12
par pouik » 18 Jan 2007, 19:12
mais je ne vois pas d'où vient ce n!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Jan 2007, 19:15
par fahr451 » 18 Jan 2007, 19:15
je dirais de ton tout premier post et de la question que tu as posée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
