Arithmétique dans Z[i]
20 messages
- Page 1 sur 1
arithmétique dans Z[i]
bonjour,
j'aimerais savoir quelles sont les notions de division euclidienne,de théorème de bezout,l théorème de gauss défini sur Z[i], notions sur Z que l'on peut transposer sur Z[i].
merci d'avance
j'aimerais savoir quelles sont les notions de division euclidienne,de théorème de bezout,l théorème de gauss défini sur Z[i], notions sur Z que l'on peut transposer sur Z[i].
merci d'avance
Bonsoir.
Tout simplement : toutes ces notions se retrouvent pour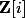 .
.
Il y a une division euclidienne : pour et
et 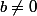 , dans
, dans 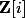 , il existe
, il existe  et
et  dans
dans 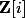 tels que
tels que 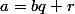 et
et 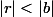 (on dit que
(on dit que 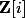 est "norme-euclidien", parce que c'est la norme qui sert de stathme euclidien).
est "norme-euclidien", parce que c'est la norme qui sert de stathme euclidien).
A partir de là,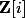 est principal (ceci est équivalent au théorème de Bezout), factoriel, etc.... tout se passe comme dans
est principal (ceci est équivalent au théorème de Bezout), factoriel, etc.... tout se passe comme dans 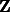 .
.
La seule différence, c'est qu'il y a quatre unités (1, -1, i et -i). Il n'y a donc plus un nombre qu'on appelle pgcd de deux nombres, c'est l'idéal engendré par ces deux nombres qu'on appelle pgcd.
Tout simplement : toutes ces notions se retrouvent pour
Il y a une division euclidienne : pour
A partir de là,
La seule différence, c'est qu'il y a quatre unités (1, -1, i et -i). Il n'y a donc plus un nombre qu'on appelle pgcd de deux nombres, c'est l'idéal engendré par ces deux nombres qu'on appelle pgcd.
Re Bonsoir.
Je reparle un peu de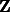 d'abord : dans
d'abord : dans 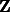 , si
, si  divise
divise  et
et  divise
divise  , on a soit
, on a soit  soit
soit 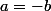 . Si on ne prend que des nombres positifs, on se débarrasse du problème et on peut dire :
. Si on ne prend que des nombres positifs, on se débarrasse du problème et on peut dire :  divise
divise  et
et  divise
divise  si et seulement si
si et seulement si  .
.
Quand au plus grand commun diviseur, il est défini de manière unique parce que l'ordre sur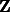 est total.
est total.
Dans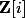 , il n'y a rien de tel : si
, il n'y a rien de tel : si  divise
divise  et
et  divise
divise  , il y a quatre possibilités :
, il y a quatre possibilités :  ,
, 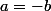 ,
, 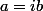 ou
ou 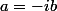 . On dit que
. On dit que  et
et  sont associés, mais aucune des quatre directions n'est privilégiée.
sont associés, mais aucune des quatre directions n'est privilégiée.
De même, il n'y a pas d'ordre naturel sur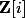 . On ne pourra donc pas parler du "plus grand" commun diviseur, parce que "plus grand" n'a pas de sens.
. On ne pourra donc pas parler du "plus grand" commun diviseur, parce que "plus grand" n'a pas de sens.
On ne peut prendre que le plus grand en norme. Mais alors il y a quatre candidats qui diffèrent d'une unité.
La solution retenue pour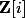 (mais aussi pour bien d'autres anneaux du même type), c'est de remplacer le pgcd de a et b par l'idéal engendré par a et b. C'est un objet unique, bien que chacun des quatre nombres dont je parlais plus haut en soit un générateur.
(mais aussi pour bien d'autres anneaux du même type), c'est de remplacer le pgcd de a et b par l'idéal engendré par a et b. C'est un objet unique, bien que chacun des quatre nombres dont je parlais plus haut en soit un générateur.
Je reparle un peu de
Quand au plus grand commun diviseur, il est défini de manière unique parce que l'ordre sur
Dans
De même, il n'y a pas d'ordre naturel sur
On ne peut prendre que le plus grand en norme. Mais alors il y a quatre candidats qui diffèrent d'une unité.
La solution retenue pour
Ah ! J'ai relu la question, et j'ai vu que tu voulais un exemple.
Alors essaye de calculer le pgcd de -7-i et de 5+i par l'algorithme d'Euclide. Tu devrais trouver 1+i. Mais au cours du calcul, tu verras que les quotients et les restes ne sont pas uniques. On a plusieurs choix. Tu pourrais aussi bien trouver 1-i, -1-i ou -1+i. Ces quatre nombres sont associés.
Alors essaye de calculer le pgcd de -7-i et de 5+i par l'algorithme d'Euclide. Tu devrais trouver 1+i. Mais au cours du calcul, tu verras que les quotients et les restes ne sont pas uniques. On a plusieurs choix. Tu pourrais aussi bien trouver 1-i, -1-i ou -1+i. Ces quatre nombres sont associés.
bonsoir,
En fait ,j'ai un petit problème pour le calcul du pgcd de -7-i et 1+5i.
Parmi plusieurs tentative j'ai:
-7-i=(5+i)*(-1)-2
5+i=-2*(-3-i)+(-1-i)
-3-i=(-1-i)*
pour cette ligne j'arrive pas a trouver un reste dont le module est inférieur à
racine de 2.
je n'arrive jamais à un reste nul .Est ce que le fait que ça bloque montre
que -1-i est le pgcd?
Est ce que tu pourrais montrer les calculs qui t'ont amené à trouver une des solutions?
merci d'avance
En fait ,j'ai un petit problème pour le calcul du pgcd de -7-i et 1+5i.
Parmi plusieurs tentative j'ai:
-7-i=(5+i)*(-1)-2
5+i=-2*(-3-i)+(-1-i)
-3-i=(-1-i)*
pour cette ligne j'arrive pas a trouver un reste dont le module est inférieur à
racine de 2.
je n'arrive jamais à un reste nul .Est ce que le fait que ça bloque montre
que -1-i est le pgcd?
Est ce que tu pourrais montrer les calculs qui t'ont amené à trouver une des solutions?
merci d'avance
Connais tu le Hardy & Wright ? La référence des références en théorie des nombres. Il y a une version scannée ici :
http://modular.fas.harvard.edu/scans/papers/hardy/Hardy-Wright-Theory_of_Numbers.pdf
Je suis sur que les chapitres XII et XIV t'intéresseraient beaucoup.
Bonne lecture, et bonne nuit !
http://modular.fas.harvard.edu/scans/papers/hardy/Hardy-Wright-Theory_of_Numbers.pdf
Je suis sur que les chapitres XII et XIV t'intéresseraient beaucoup.
Bonne lecture, et bonne nuit !
Salut, je ne suis pas expert en algèbre, mais quelque chose me frappe:
Si Z[i] est principal, l'idéal engendré par nos deux nombre est lui même principal, non? Donc on peut trouver un unique générateur. Pourquoi ne peut on pas dire que c'est lui le pgcd? (ou un pgcd parce qu'il n'y a probablement pas d'unicité)
A+
redwolf a écrit:A partir de là,est principal [...]
Il n'y a donc plus un nombre qu'on appelle pgcd de deux nombres, c'est l'idéal engendré par ces deux nombres qu'on appelle pgcd.
Si Z[i] est principal, l'idéal engendré par nos deux nombre est lui même principal, non? Donc on peut trouver un unique générateur. Pourquoi ne peut on pas dire que c'est lui le pgcd? (ou un pgcd parce qu'il n'y a probablement pas d'unicité)
A+
Bonjour.
Quinto, tu réponds à ta propre question. Il n'y a pas un unique générateur pour un idéal principal. Dans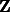 déjà, il y a deux générateurs par idéal non nul, et on dit "le pgcd" parce qu'il y a une direction privilégiée (la direction positive).
déjà, il y a deux générateurs par idéal non nul, et on dit "le pgcd" parce qu'il y a une direction privilégiée (la direction positive).
Dans d'autres anneaux, chaque générateur peut être appellé "un pgcd" mais aucun ne mérite le titre "le pgcd".
Dans des anneaux principaux plus exotiques que Z ou Z[i], "pgcd" ne veut vraiment plus rien dire, parce qu'il n'y a même pas de norme pour laquelle il soit "plus grand" que les autres.
Le bon objet est bien + : la somme des idéaux engendrés par a et b.
Quinto, tu réponds à ta propre question. Il n'y a pas un unique générateur pour un idéal principal. Dans
Dans d'autres anneaux, chaque générateur peut être appellé "un pgcd" mais aucun ne mérite le titre "le pgcd".
Dans des anneaux principaux plus exotiques que Z ou Z[i], "pgcd" ne veut vraiment plus rien dire, parce qu'il n'y a même pas de norme pour laquelle il soit "plus grand" que les autres.
Le bon objet est bien + : la somme des idéaux engendrés par a et b.
Bonsoir.
Quinto n'a pas tort cependant. L'intérêt des anneaux principaux, c'est que les idéaux coïncident avec les éléments. Les unités ne sont pas un obstacle et on peut dire (comme le dit Redwolf) que "le" PGCD est -1+i ou -1-i.
Les idéaux sont indispensables pour faire de l'arithmétique dés que l'anneau n'est plus principal comme Z[irac(5)].
Quinto n'a pas tort cependant. L'intérêt des anneaux principaux, c'est que les idéaux coïncident avec les éléments. Les unités ne sont pas un obstacle et on peut dire (comme le dit Redwolf) que "le" PGCD est -1+i ou -1-i.
Les idéaux sont indispensables pour faire de l'arithmétique dés que l'anneau n'est plus principal comme Z[irac(5)].
Bonjour,
j'essaie de démontrer le résultat suivant
Un entier est somme de deux carrés si et seulement si les nombres premiers congrus à 3 modulo 4 qui le divisent ont une valuation paire.
j'ai trouvé un exo qui utilise les entiers de gauss avoir ce résultat.
D'abord on démontre que si x et y sont somme de 2 carrés alors le produit aussi (facile)
Ensuite on montre que si un nombre premier impair est somme de 2 carrés il est nécessairement de la forme 4k+1 (je l'ai fait )
Ensuite, on suppose p de la forme 4k+1 et on veut montrer que p est somme de 2 carrés .Puis sachant qu'il y a un entier n tel que p/1+n^2 ,n entre 1 et p-1
Considérant,le pgcd d de n+i et p on doit montrer que p est bien somme de 2 carrés.Ce que je n'arrive pas à faire .Voilà ce que j'ai
d=a+ib divise p donc mp donc n^2+1, d divise (n+i)(n-i) je pense qu'il faut montrer que p=a^2+b^2
en considérant d'=a-ib (pgcd de p et n-i?)
Enfin à partir de là comment en déduire le résultat, i.e. tout entier est somme de 2 carrés ssi tout nombre premier 4k+3 à une puissance paire dans sa décomposition en facteurs premiers.
merci d'avance à ceux qui voudront m'aider
j'essaie de démontrer le résultat suivant
Un entier est somme de deux carrés si et seulement si les nombres premiers congrus à 3 modulo 4 qui le divisent ont une valuation paire.
j'ai trouvé un exo qui utilise les entiers de gauss avoir ce résultat.
D'abord on démontre que si x et y sont somme de 2 carrés alors le produit aussi (facile)
Ensuite on montre que si un nombre premier impair est somme de 2 carrés il est nécessairement de la forme 4k+1 (je l'ai fait )
Ensuite, on suppose p de la forme 4k+1 et on veut montrer que p est somme de 2 carrés .Puis sachant qu'il y a un entier n tel que p/1+n^2 ,n entre 1 et p-1
Considérant,le pgcd d de n+i et p on doit montrer que p est bien somme de 2 carrés.Ce que je n'arrive pas à faire .Voilà ce que j'ai
d=a+ib divise p donc mp donc n^2+1, d divise (n+i)(n-i) je pense qu'il faut montrer que p=a^2+b^2
en considérant d'=a-ib (pgcd de p et n-i?)
Enfin à partir de là comment en déduire le résultat, i.e. tout entier est somme de 2 carrés ssi tout nombre premier 4k+3 à une puissance paire dans sa décomposition en facteurs premiers.
merci d'avance à ceux qui voudront m'aider
Bonjour.
d ne peut être égal à p, sans quoi on aurait p divise n+i, ce qui est faux puisque 1/p n'est pas un entier.
d ne peut être égal à 1, car p serait alors premier avec n+i, donc aussi avec n-i (par conjugaison) et donc aussi avec leur produit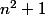 .
.
Mais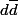 divise
divise 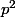 dans
dans 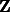 . D'après ce qui précède,
. D'après ce qui précède, 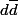 ne peut être égal ni à
ne peut être égal ni à 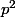 (car d serait associé à p) ni à 1 (car d serait associé à 1).
(car d serait associé à p) ni à 1 (car d serait associé à 1).
C'est donc que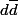 est égal à p, c'est-à-dire :
est égal à p, c'est-à-dire :
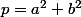 .
.
d ne peut être égal à p, sans quoi on aurait p divise n+i, ce qui est faux puisque 1/p n'est pas un entier.
d ne peut être égal à 1, car p serait alors premier avec n+i, donc aussi avec n-i (par conjugaison) et donc aussi avec leur produit
Mais
C'est donc que
1) Apparemment, tu sais faire l'existence de n tel que p|n²+1 ??
2) Si d=1, alors d'après Gauss, d|n-i, puis en conjuguant, d|n+i . C'est absurde. Ainsi d est différent de 1. On pose d=a+bi et on a donc
p=(a+bi)(c+di) où a+bi et c+di sont des entiers de Gauss autres que des unités.
En prenant les modules au carré : p²=(a²+b²)(c²+d²). On a ici un produit dans Z. Le premier membre est une décomposition en facteurs premiers, et les deux facteurs du second membre sont différents de 1, donc ils valent chacun p. (C'est bien ce que tu pensais : p=(a+bi)(a-bi)).
3) Soit N un entier dont les facteurs premiers congrus à 3 modulo 4 sont de valuations paires. Alors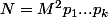 , où les
, où les  sont les premiers congrus à 1 modulo 4, et où M² regroupe les autres facteurs. On a chaque
sont les premiers congrus à 1 modulo 4, et où M² regroupe les autres facteurs. On a chaque  qui est somme de deux carrés, donc leur produit aussi et finalement N aussi.
qui est somme de deux carrés, donc leur produit aussi et finalement N aussi.
Réciproquement, il faut supposer qu'un premier congru à 3 modulo 4 apparait avec une valuation impaire et montrer que N e peut être somme de deux carrés et là je ne vois pas dans l'immédiat, mais cela ne doit pas être dur.
2) Si d=1, alors d'après Gauss, d|n-i, puis en conjuguant, d|n+i . C'est absurde. Ainsi d est différent de 1. On pose d=a+bi et on a donc
p=(a+bi)(c+di) où a+bi et c+di sont des entiers de Gauss autres que des unités.
En prenant les modules au carré : p²=(a²+b²)(c²+d²). On a ici un produit dans Z. Le premier membre est une décomposition en facteurs premiers, et les deux facteurs du second membre sont différents de 1, donc ils valent chacun p. (C'est bien ce que tu pensais : p=(a+bi)(a-bi)).
3) Soit N un entier dont les facteurs premiers congrus à 3 modulo 4 sont de valuations paires. Alors
Réciproquement, il faut supposer qu'un premier congru à 3 modulo 4 apparait avec une valuation impaire et montrer que N e peut être somme de deux carrés et là je ne vois pas dans l'immédiat, mais cela ne doit pas être dur.
Voici l'argument de Hardy & Wright concernant le dernier point qu'évoque yos :
1) Si p=4m+3, p divise n et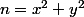 alors x et y ne peuvent pas être premiers entre eux.
alors x et y ne peuvent pas être premiers entre eux.
Si c'était le cas, p ne pourrait diviser ni x ni y. Il y aurait donc un entier z tel que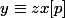 et on aurait
et on aurait \equiv 0[p]) .
.
D'où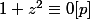 , et c'est une contradiction, puisque -1 n'est pas un carré modulo p.
, et c'est une contradiction, puisque -1 n'est pas un carré modulo p.
2) Toujours avec p=4m+3 et p divsant n : on appelle c l'exposant de p dans n et on suppose que c est impair. Supposons que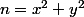 . Posons d=pgcd(x,y) et
. Posons d=pgcd(x,y) et  l'exposant de p dans d.
l'exposant de p dans d.
) avec X et Y premiers entre eux. Posons
avec X et Y premiers entre eux. Posons 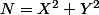 . p divise N
. p divise N 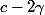 fois et
fois et 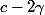 ne peut pas être nul parce que c est impair. p divise donc N et
ne peut pas être nul parce que c est impair. p divise donc N et 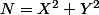 avec X et Y premiers entre eux. Ceci contredit le 1).
avec X et Y premiers entre eux. Ceci contredit le 1).
1) Si p=4m+3, p divise n et
Si c'était le cas, p ne pourrait diviser ni x ni y. Il y aurait donc un entier z tel que
D'où
2) Toujours avec p=4m+3 et p divsant n : on appelle c l'exposant de p dans n et on suppose que c est impair. Supposons que
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
