Ah, O.K., je pense comprendre où se situe le problème.
La paramétrisation de l'ellipse avec laquelle tu travaille, c'est
,b\sin(t)\big))
et toi, j'ai bien l'impression que tu fait comme si le

de cette paramétrisation correspondait à quelque chose de "concret" (et de simple) sur l'ellipse, à savoir un angle ou bien une longueur.
Bon, ben je te rassure, le

en question, il ne correspond ni à un angle (mesuré où que ce soit sur l'ellipse) ni à une longueur (mesurée où que ce soit sur l'ellipse).
Donc si tu veut "couper" un quart d'ellipse en 5 portions
de même longueur, ben ça ne correspond absolument pas à couper l'intervalle dans lequel

se balade, à savoir
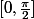
en 5 intervalle
de même longueur. Et ça ne correspond pas non plus si tu veut couper ton quart d'ellipse en 5 morceaux correspondant à 5 secteurs angulaires de même angle.
Et la raison de tout ça, c'est que, certes sur le cercle trigo. paramétré par
,\sin(t)\big))
, le

il correspond bien à un angle et à une longueur (la longueur de l'arc). Sauf que, pour passer de ce cercle à ton ellipse, tu "étire" l'axe des x et celui des y
selon des facteurs différents ce qui modifie complètement les longueurs et les angles (et pas par un bête rapport multiplicatif vu qu'au départ, sur le cercle, la largeur et la hauteur étaient les mêmes alors qu'à l'arrivée c'est plus le cas)
