bonjour
comment puis-je montrer qu'il existe un isomorphisme de R[x]/(x²+x+1) dans C
merci
Anneau quotient isomorphisme
7 messages
- Page 1 sur 1
bonjour merci pour vos réponses
voici une réponse que j'ai faite.. est elle convenable
j'ai poser G : R[x] -> C qui a pas associe P(j)
G est un morphisme d'anneaux, c'est aussi un morphisme de R-espace vectoriel il est surjectif car G est une application linéaire et que i et 1 sont dans Im(G) avec (i,1) base du R espace vectoriel
Mais comme P est à coeficient réels s'il admet j comme racin,e, il admet aussi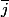 , conjugué de j
, conjugué de j
il est donc divisble par
(x-j)(x-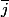 ) = x²+x+1
) = x²+x+1
et réciproquement tout polynôme multiple de x²+x+1 est dans le noyau
d'aprés le théorème d'isomorphisme on a le résultat cherché
et j'auais une autre question svp
j'ai un polynome P(x) =x^3+x+1,
j'ai montré qu'il possédait une racine réelle a, il faut que j'en déduise R[x]/(P) est isomorphe a R x C par le théoréme chinois pour R[x] mais je n'arrive pas a retranscrire le théorème chinois pour R[x]...
voici une réponse que j'ai faite.. est elle convenable
j'ai poser G : R[x] -> C qui a pas associe P(j)
G est un morphisme d'anneaux, c'est aussi un morphisme de R-espace vectoriel il est surjectif car G est une application linéaire et que i et 1 sont dans Im(G) avec (i,1) base du R espace vectoriel
Mais comme P est à coeficient réels s'il admet j comme racin,e, il admet aussi
il est donc divisble par
(x-j)(x-
et réciproquement tout polynôme multiple de x²+x+1 est dans le noyau
d'aprés le théorème d'isomorphisme on a le résultat cherché
et j'auais une autre question svp
j'ai un polynome P(x) =x^3+x+1,
j'ai montré qu'il possédait une racine réelle a, il faut que j'en déduise R[x]/(P) est isomorphe a R x C par le théoréme chinois pour R[x] mais je n'arrive pas a retranscrire le théorème chinois pour R[x]...
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
