Questions sur un anneau quotient
54 messages
- Page 2 sur 3 - 1, 2, 3
Re: Questions sur un anneau quotient
-Pour que f soit injectif il faut et suffit que Ker(f) soit réduit à l'élément neutre de G.
-Si G est abelien additif, alors G/Ker(f) est isomorphe à f(G) via l'application qui a x+Ker(f) associe f(x)
-Si G est abelien additif, alors G/Ker(f) est isomorphe à f(G) via l'application qui a x+Ker(f) associe f(x)
Re: Questions sur un anneau quotient
Et il n'est absolument pas utile que G soit abélien : de toute façon Ker(f) est forcément un sous groupe distingué de G (donc G/Ker(f) est un groupe) et le morphisme f se "factorise" systématiquement en un isomorphisme de G/Ker(f)->Im(f).ArtyB a écrit:-Si G est abelien additif, alors G/Ker(f) est isomorphe à f(G) via l'application qui a x+Ker(f) associe f(x) <= OUI !!!!
C'est ce qu'on appelle en général "le premier théorème d'isomorphisme" et évidement, on l'utilise dans quasi tout les trucs qui concernent les groupes.
Et ici, ça te dit quoi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Questions sur un anneau quotient
Et beh j'apprends beaucoup plus en un post sur ce forum qu'en plusieurs jours à lire mon cours et faire mes exercices. Je ne me suis jamais mais alors jamais servi de ce théorème !
En revenant dans notre cas, cela nous dit que le groupe K*/Ker(f)=(x \in {-1, 1}) est isomorphe à f(K*)=H mais je ne vois toujours pas le rapport avec le cardinal
En revenant dans notre cas, cela nous dit que le groupe K*/Ker(f)=(x \in {-1, 1}) est isomorphe à f(K*)=H mais je ne vois toujours pas le rapport avec le cardinal
Re: Questions sur un anneau quotient
Essaie de réfléchir au lieu de dire systématiquement que tu ne vois pas le rapport.
Quel est le cardinal du quotient K*/{-1,1} ?
Si deux groupes sont isomorphes, que peut-on dire de leurs cardinaux ?
Quel est le cardinal du quotient K*/{-1,1} ?
Si deux groupes sont isomorphes, que peut-on dire de leurs cardinaux ?
Re: Questions sur un anneau quotient
K*/{-1,1} est isomorphe à H et est donc de même cardinal que H.
K* est d'ordre 26, donc l'ordre de K*/{-1,1} (ie l'ordre de H) divise 26.
|K*/{-1,1}|=|K*|/|{-1,1}|=26/2=13
donc H est d'ordre 13.
C'est ça ?
K* est d'ordre 26, donc l'ordre de K*/{-1,1} (ie l'ordre de H) divise 26.
|K*/{-1,1}|=|K*|/|{-1,1}|=26/2=13
donc H est d'ordre 13.
C'est ça ?
Re: Questions sur un anneau quotient
Oui, après une nuit à passer à relire mon cours, à le comprendre, à redémontrer, à prendre des exemples, à essayer d'appliquer mon cours je l'ai enfin compris !
Question suivante: 9) Montrer que a appartient à H. Pour le démontrer, il faut démontrer que a est un carré d'éléments de K*.
Puisque K* est cyclique, H est l'unique sous groupe d'ordre 13 de K*. Or a^13=1 donc a est bien un élément de H ?
Question suivante: 9) Montrer que a appartient à H. Pour le démontrer, il faut démontrer que a est un carré d'éléments de K*.
Puisque K* est cyclique, H est l'unique sous groupe d'ordre 13 de K*. Or a^13=1 donc a est bien un élément de H ?
Re: Questions sur un anneau quotient
En gros ça, préciser l'argument (tout repose en effet sur la cyclicité).
Re: Questions sur un anneau quotient
Comme K* est cyclique d'ordre 26, l'application qui a d associe Hd est une bijection entre l'ensemble des diviseurs positifs
de 26 et l'ensemble des sous-groupes de K*. En particulier, pour tout diviseur d de 26,
Hd est l'unique sous-groupe d'ordre d de K*. Donc H est l'unique sous groupe d'ordre 13 de de K*. Et H est l'ensemble des éléments x de K* qui vérifient x^13=1 (car l'élément neutre est 1) donc comme a^13=1, a appartient à H.
Là où j'ai du mal c'est pour résoudre l'équation Y²-a=0, ie Y²=a (où Y est en élément de K[Y]), comment trouver les racines dans K ?
Il faut trouver les éléments x de K qui vérifient x²=a, or on a a^13=1 donc a^14=a et on prend la racine carrée de a^14 ?
de 26 et l'ensemble des sous-groupes de K*. En particulier, pour tout diviseur d de 26,
Hd est l'unique sous-groupe d'ordre d de K*. Donc H est l'unique sous groupe d'ordre 13 de de K*. Et H est l'ensemble des éléments x de K* qui vérifient x^13=1 (car l'élément neutre est 1) donc comme a^13=1, a appartient à H.
Là où j'ai du mal c'est pour résoudre l'équation Y²-a=0, ie Y²=a (où Y est en élément de K[Y]), comment trouver les racines dans K ?
Il faut trouver les éléments x de K qui vérifient x²=a, or on a a^13=1 donc a^14=a et on prend la racine carrée de a^14 ?
Re: Questions sur un anneau quotient
Je ne sais pas justement, c'est ce à quoi je suis arrivé en tatonant mais bon ça n'est pas concluant.
En fait je n'arrive pas à voir comment trouver les éléments x tels que x²=a.
Je sais que a appartient à H et donc que a est un carré et que les éléments x vérifiant x²=a se trouvent donc dans K* mais ensuite je bloque.
En fait je n'arrive pas à voir comment trouver les éléments x tels que x²=a.
Je sais que a appartient à H et donc que a est un carré et que les éléments x vérifiant x²=a se trouvent donc dans K* mais ensuite je bloque.
Re: Questions sur un anneau quotient
Ton idée était bonne, je voulais simplement te faire préciser les racines carrées de  ! (L'une d'entre elles engendre
! (L'une d'entre elles engendre 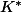 ).
).
Re: Questions sur un anneau quotient
Au temps pour moi alors !
Un générateur de K* est un élément x de K* tel que l'ordre de x soit égal à l'ordre de K*, ie un élément x d'ordre 26.
Bon alors les racines de a^14 sont les x tels que x^2=a^14 mais là euh je sèche un peu, comment les trouver ?
Un générateur de K* est un élément x de K* tel que l'ordre de x soit égal à l'ordre de K*, ie un élément x d'ordre 26.
Bon alors les racines de a^14 sont les x tels que x^2=a^14 mais là euh je sèche un peu, comment les trouver ?
Re: Questions sur un anneau quotient
Ah si pour le coup, je suis bien réveillé. Mais je ne vois pas en quoi l'élément x de K* dont l'ordre est 26 est une racine de a^14.
K* étant composé des éléments d'ordre 1, 2, 13 et 26 on cherche un élément de l'un de ces ordres tel que son carré sont a^14.
Alors c'est peut être une évidence qui pend juste sous mon nez mais je ne la vois pas.
A part a^7 (car (a^7)^2=a^14=a) je ne vois pas trop quelles sont les autres racines de a^14, (-a^7) peut être ?
K* étant composé des éléments d'ordre 1, 2, 13 et 26 on cherche un élément de l'un de ces ordres tel que son carré sont a^14.
Alors c'est peut être une évidence qui pend juste sous mon nez mais je ne la vois pas.
A part a^7 (car (a^7)^2=a^14=a) je ne vois pas trop quelles sont les autres racines de a^14, (-a^7) peut être ?
Re: Questions sur un anneau quotient
En fait les deux seules racines possibles sont a^7 et -a^7=2a^7 car -1 congrue à 2 modulo 3. Ensuite il ne me reste qu'à exprimer leurs coordonnées dans B.
Question 11 montrer que 2a est un générateur de K*.
K* étant d'autre 26, il faut que (2a)^26 soit différent de 1, c'est bien ça ?
Question 11 montrer que 2a est un générateur de K*.
K* étant d'autre 26, il faut que (2a)^26 soit différent de 1, c'est bien ça ?
Re: Questions sur un anneau quotient
2a est générateur de K* si tout élément de K* peut s'écrire comme un multiple de 2a.
Si g est générateur de K*, alors g^(n/d) générateur de H avec n l'ordre de K* et d l'ordre de H.
Ici K* d'ordre 26, et H d'ordre 13 (n/d=2), donc si g^2 générateur de H, g est un générateur de K*.
En écrivant g sous la forme g=2a, si (2a)^2 est un générateur de H, alors 2a est un générateur de K*
Si g est générateur de K*, alors g^(n/d) générateur de H avec n l'ordre de K* et d l'ordre de H.
Ici K* d'ordre 26, et H d'ordre 13 (n/d=2), donc si g^2 générateur de H, g est un générateur de K*.
En écrivant g sous la forme g=2a, si (2a)^2 est un générateur de H, alors 2a est un générateur de K*
Re: Questions sur un anneau quotient
ArtyB a écrit:...si g^2 générateur de H, g est un générateur de K* <= FAUX
Il te faut une condition supplémentaire (et je te donne pas de contre exemple vu que tu en as un sous les yeux, à savoir g=...)
Sinon, une indication : tu ferais nettement mieux de garder -a plutôt que 2a vu que (-a)^n semble plus "sympathique" que (2a)^n...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
54 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
