Bonjour !
Je me demandais si il était vrai de dire que :
"la fonction est uniformément continue sur I" et "la dérivée de la fonction est bornée sur I" sont des propositions équivalentes, dans le cadre de fonctions dérivables évidemment, et avec I un intervalle ouvert, une fonction dérivable étant uniformément continue sur un intervalle fermé (si je ne me trompes pas...).
L'équivalence me semble vraie mais je n'arrive pas à la montrer.
Quelqu'un peut m'aider ?
Merci d'avance.
Analyse : lien entre uniforme continuité et dérivée
8 messages
- Page 1 sur 1
Re: analyse : lien entre uniforme continuité et dérivée
Bonjour,
une fonction f dont la dérivée est bornée est lipschitzienne donc uniformément continue (écrire f(y)-f(x) sous forme d'intégrale).
En revanche, la fonction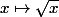 sur
sur 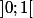 est uniformément continue (elle est continue sur le compact
est uniformément continue (elle est continue sur le compact  ) mais sa dérivée
) mais sa dérivée 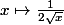 n'est pas bornée (elle tend vers l'infini mais très lentement au voisinage de 0).
n'est pas bornée (elle tend vers l'infini mais très lentement au voisinage de 0).
Il faudrait donc remplacer "uniformément continue" par "lipschitzienne", et là ça marche.
une fonction f dont la dérivée est bornée est lipschitzienne donc uniformément continue (écrire f(y)-f(x) sous forme d'intégrale).
En revanche, la fonction
Il faudrait donc remplacer "uniformément continue" par "lipschitzienne", et là ça marche.
Re: analyse : lien entre uniforme continuité et dérivée
D'accord merci beaucoup pour cette réponse !
Re: analyse : lien entre uniforme continuité et dérivée
Et aurais-tu une idée pour démontrer l'équivalence fonction liepschitz/dérivée bornée ?
Re: analyse : lien entre uniforme continuité et dérivée
Soit 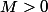 alors
alors
| \leq M \iff \forall x,y \in I,~ |f(x)-f(y)| \leq M|x-y|)
=> utiliser-f(y) = \int_x^y f'(t)dt) .
.
<= montrer que tous les taux de variation de en
en 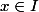 sont bornés par
sont bornés par  et en déduire que
et en déduire que ) aussi.
aussi.
=> utiliser
<= montrer que tous les taux de variation de
Re: analyse : lien entre uniforme continuité et dérivée
Bonjour,
Ou bien : taux d'accroissement et passage à la limite : pour donné dans I,
donné dans I, -f(x_0)}{x-x_0} \leq M) , donc limite quand
, donc limite quand 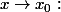
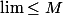 , donc
, donc  \leq M)
Ou bien : taux d'accroissement et passage à la limite : pour
Re: analyse : lien entre uniforme continuité et dérivée
Merci beaucoup à vous deux j'ai compris maintenant ! 
Re: analyse : lien entre uniforme continuité et dérivée
Ca m'a merveilleusement servi pendant mes partielles d'analyse encore merci !
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
