Pb d'analyse complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
luke
- Messages: 5
- Enregistré le: 18 Juin 2008, 10:44
-
 par luke » 18 Juin 2008, 10:51
par luke » 18 Juin 2008, 10:51
Bonjour,
je cherche une demonstration de l'inegalite suivante :
pour p complexe a partie reelle positive

Geometriquement, on "voit" que la fonction

est inscrite dans le cercle de rayon 3/4 de centre 1/4
merci
Luke
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 18 Juin 2008, 18:10
par tize » 18 Juin 2008, 18:10
Salut,
je ne sais pas quel est la marche à suivre pour ce genre de problème (et j'ai souvent tendance à me dire: pourquoi la variable n'est pas réelle ?) mais voilà un début :
première remarque :
Si P est le demi plan des complexes à partie réelle positive alors l'image de P par

est le disque unité. et donc

l'inégalité cherchée est donc vraie dès que

reste à voir que cela est vrai aussi pour |p|<4 et p dans P. Or on a une fonction complexe qui doit donc atteindre son maximum (en module) sur le bord du demi disque. Sur le demi cercle on sait déjà que la fonction est inférieur (en module) à 3/4 reste à trouver le maximum sur le segment [-4i ; 4i ]. i.e. le maximum pour |y|<4 de
}{y/2}e^{-iy/2}-1/4|)
. Je me suis dit que ça ne devait pas être trop dur...mais j'ai pas fait...
Bon courage pour la suite.
-
mathelot
 par mathelot » 18 Juin 2008, 19:57
par mathelot » 18 Juin 2008, 19:57
Bonsoir,
autre démo.
Dans
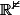
, il n'y a plus de théorème des accroissements finis mais subsiste une
inégalité des accroissement finis.

est un "taux d'accroissement" d'une fonction holomorphe.
D'où si
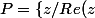 \geq 0 \})
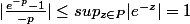
d'où
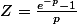
appartient au disque unité fermé
)
pour
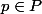
.
L'inégalité en découle car la distance de

à
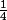
est plus petite que
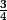
-
luke
- Messages: 5
- Enregistré le: 18 Juin 2008, 10:44
-
 par luke » 19 Juin 2008, 12:58
par luke » 19 Juin 2008, 12:58
Rebonjour,
Merci pour les demos.
J'ai bien compris que

etait de module inférieur à 1.
Par contre, je ne vois pas pourquoi cela implique que l'inégalité recherchée est vraie.
A bientôt,
Luke
-
mathelot
 par mathelot » 19 Juin 2008, 17:30
par mathelot » 19 Juin 2008, 17:30
luke a écrit:Par contre, je ne vois pas pourquoi cela implique que l'inégalité recherchée est vraie.
tu as raison. j'ai écrit des bêtises. L'exercice n'est pas facile :hum:
les choses sûres pour l'instant:

appartient au disque unité et

aussi.
peut être pourrait on utiliser une différence finie d'ordre 2 ?
(un taux d'accroissement de taux d'acroissements) ou
une majoration du théorème des accroissements finis
sur un segment tp pour
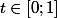
et
)
puisque le disque est convexe ?
-
luke
- Messages: 5
- Enregistré le: 18 Juin 2008, 10:44
-
 par luke » 19 Juin 2008, 20:25
par luke » 19 Juin 2008, 20:25
Je vais essayer d'utiliser un ordre 2 et ceci d'autant plus que le cercle de centre 1/4 et de rayon 3/4 est aussi le cercle osculateur de la courbe

au point w=0.
Comme le propose tize, comme la fonction est holomorphe, peut-etre faut-il considerer l'axe des imaginaires seulement, droite pour laquelle la fonction atteint son maximum.
Luke
-
mathelot
 par mathelot » 19 Juin 2008, 20:32
par mathelot » 19 Juin 2008, 20:32
j'ai regardé pour p=x réel positif.
Le module de

est décroissant de
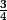
vers zéro quand
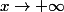
oui, relis ce qu'a écrit Tize, c'est nickel. Il a utilisé le principe du maximum
pour une fonction holomorphe et a ramené le problème
à l'étude toute simple d'une fonction à variable réelle y sur le segment [-4;4].
-
luke
- Messages: 5
- Enregistré le: 18 Juin 2008, 10:44
-
 par luke » 19 Juin 2008, 21:06
par luke » 19 Juin 2008, 21:06
En fait, la methode de tize conduit a l'analyse d'une fonction un peu complique , non?
on cherche le module d'une fonction complexe (présence de l'exponentielle complexe).
Luke
-
mathelot
 par mathelot » 19 Juin 2008, 22:10
par mathelot » 19 Juin 2008, 22:10
tize a écrit:Sur le demi cercle on sait déjà que la fonction est inférieur (en module) à 3/4 reste à trouver le maximum sur le segment [-4i ; 4i ]. i.e. le maximum pour |y|<4 de
}{y/2}e^{-iy/2}-1/4|)
je commence les calculs avec la formule complexe:
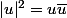
l'inégalité équivaut à
)-y^2-y\sin(y) \leq 0)
vérification à la calculatrice , c'est ok. Pas étonnant que l'exercice
soit difficile: le contact en zéro a l'air d'être d'ordre 4.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités