salut,
3b)
}{\partial \bar{z}} = \frac{\partial f}{\partial \bar{z}} \bar{f} + \frac{\partial \bar{f}}{\partial \bar{z}} f)

car f est holomorphe.
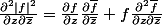
en ayant dérivé le produit.
avec un peu de chance,
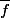
est harmonique, donc:

mais:

comme on le voit en développant localement en série entière.
d'où:

d'où si

, alors f=constante d'après 2.
3) supposons Re(f)=k sur U.
 = \frac{1}{2} (f + \bar{f}))
en dérivant par rapport à
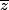
:
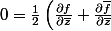)
or:

car f est holomorphe.


donc f est constante sur U.
4)
=f(\bar{z}))
en dérivant par rapport à z:
=f ' (\bar{z}) \frac{\partial \bar{z}}{\partial z}=0)
donc f est constante sur U.
PS: voilà comment je perçois les notations:
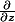
et

sont deux opérateurs formels , définis à partir des dérivées
partielles de f,
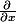
et

, même quand la fonction f de deux variables réelles x et y n'est pas fonction de z et de
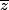
, c'est à dire même quand f n'est pas holomorphe et sa conjuguée non plus. Ceci dit, ces notations sont bien pratiques car si f est holomorphe,
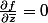
et
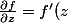)

