Bonjour,
J'ai un exercice d'analyse complexe (voir ci-attaché).
https://www.cjoint.com/c/KLdnkBz6Pk6Voici mes réponses:
1- si k=1 , alors f(z)=f(z), donc

est l'ensemble des fonctions holomorphes sur le disque D(0, R).
2- On a
= f(0)^k)
, donc
\vert =\vert f(0)\vert^k)
, par suite
\vert=1)
ou
\vert^{k-1}=1)
, d’où le résultat.
3- On montre par récurrence que
=(f(z))^{k^n})
pour tout n et pour tout z dans le disque D(0, 1).
Le terme à gauche tend vers f(0) lorsque n tend vers

. Ainsi la suite
)^{k^n})_n)
est convergente et par suite elle est bornée. comme sa limite
\vert \leq 1)
, alors à partir d'un certain rang
)^{k^n})\vert \leq 1)
, ce qui donne que
\vert \leq 1)
si z est dans D(0, 1).
4- Soit z dans D(0, 1). On a
\vert\leq 1=\vert f(0)\vert)
. Par le principe du maximum, f est constante sur D(0,1), ainsi f est constante sur D(0,R) par le principe des zéros isolés.
On a
\vert=1)
, donc il existe
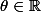
tel que
=e^{i\theta})
et par suite
=f(0)=f(0)^k=e^{i\theta k})
.
5-a- Comme f(0)=0, alors 0 est un zéro de f d'ordre au moins 1, donc il existe
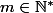
et une fonction g holomorphe sur D(0,R) vérifiant
\neq 0)
et
=z^m g(z))
.
Mes réponses sont-elles correctes?
Pouvez vous m'aider à résoudre les questions restantes 5-b ) et 6)?
Merci beaucoup d'avance.
Cordialement,
Sylvain
