Analyse complexe

par **manelrj** » 08 Mar 2018, 19:09

bonsoir a tous est ce que vous pouvez m'aider de savoir pourquoi une fonction holomorphe de classe C1 est de classe infini ???

par **Elias** » 08 Mar 2018, 19:59

Salut,

Ta question est plutôt: expliquer pourquoi si

est un ouvert de

et si

est holomorphe sur

(c'est à dire dérivable au sens complexe en tout point de

), alors

est indéfiniment dérivable au sens complexe en tout point de

.

Cela provient du fait qu'une telle fonction f est forcément analityque sur

. Cela signifie que pour tout

, il existe une suite

de nombres complexes et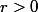

tel que pour tout

dans le disque

(contenu dans

), on a :

Ainsi, f est développable en série entière en tout point de

. Il est facile de voir qu'elle est alors indéfiniment dérivable en tout point (comme on fait pour les séries entières).