Algèbre !!

par **Elvis** » 11 Déc 2007, 22:16

Bonsoir à tous,

Petit problème d'algèbre ... grand soucis ! Le voici :
" Combien d'anneaux commutatifs (unitaires) y a-t-il, à isomorphisme près, de cardinal 0,...,6"

Je crois que c'est à peu près bon jusqu'à 4 (encore que 4 a l'air instable !), c'est après que ça se corse ! Si vous pouviez me prêter mains fortes ...
Merci d'avance.

par **Elvis** » 11 Déc 2007, 22:59

Pas de petit coup de pouce ce soir ? Tant pis, je retente ma chance demain aux aurores ! :we:

par **ThSQ** » 11 Déc 2007, 23:02

Les groupes commutatifs on les connait parfaitement non ?

Bon 0,1 et 2 je t'accorde que c'est pas excitant.
Maintenant il faut coller une multiplication dessus.
Donc ça fait à mon avis (pas de détails bicose dodo + DS Maths demain) :
4 : Z/2Z² et Z/4Z
5 : Z/5Z (qui se paye le luxe d'être un corps, tant qu'à faire)
6 : Z/2Z x Z/3Z (un seul)

par **Elvis** » 11 Déc 2007, 23:16

Je vais méditer tout ça. Réponse demain ... Et merci

par **Elvis** » 12 Déc 2007, 17:55

Bonsoir, bonsoir,

Est ce qu'il serait possible d'avoir davantage d'explications sur la réponse de ThSQ. Merci d'avance.

par **ThSQ** » 12 Déc 2007, 19:08

Ouais ça intéresse pas grand monde pourtant c'est amusant :++:

D'ailleurs j'en ai oublié un, le corps (de Galois pour ceusses qui se la pêtent :we:) à 4 éléments !!

Y'a surement plus malin mais j'ai juste regardé bêtement quelle multiplication on pouvait mettre sur les groupes commutatifs connus.

par **Elvis** » 12 Déc 2007, 19:16

C'est vrai que ya pas grand monde qui réagit.
Mon problème est le suivant : si on considère un élément à 4 élements X = {0,x,y,z} avec 0 élement neutre pour l'addition. Il y a 4 choix pour 0 puis 3 choix pour l'élément neutre 1 de la multiplication. Donc je ne comprends pas trop comment tu trouves 2 solutions pour les groupes commutatifs ... Je sais pas si j'ai bien expliqué mon problème ...

par **Elvis** » 12 Déc 2007, 20:44

Pas de volontaires pour quelques explications ??

par **Elvis** » 12 Déc 2007, 20:56

Toujours personne pour m'expliquer le procédé ??

par **ThSQ** » 12 Déc 2007, 21:35

Bon, je fais comme ça mais je te garantis pas que c'est la méthode la plus 'stucieuse ....

Anneaux à 4 éléments : R = ({ 0, 1, a, b=1+a }, +, .)

1. Si (R,+) ~= Z/2Z²,+
x + x = 0 pour tout x

1.1 si ab=0
alors ab + b= b(a+1) = b² = b
pareil pour a² = A
etc...

Au final R = Z/2Z²

1.2 si ab=1 (j'avais zoublié ce cas là hier soir)
ab = a(a+1) = a²+a = 1 soit a² = 1-a=1+a=b
pareil b²=a
etc..

Au final R =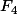

, corps de Galois à 4 éléments.

1.3 si ab=a=-a ou ab=b
en bidouillant on arrive à une contradiction

2. 1. Si (R,+) ~= Z/4Z,+
en bidouillant on arrive à R = anneau Z/4Z

......

par **Elvis** » 12 Déc 2007, 21:47

Je sais que ma question est lourde, mais je pensais au début, chercher les groupes commutatifs et ensuite mettre une multiplication associative, distributive et commutative. Et j'ai du mal à faire le rapprochement avec tes explications ... Désolé ! :stupid_in

par **ThSQ** » 12 Déc 2007, 21:56

Je suis désolé Elvis si c'est pas clair. Je sais pas l'expliquer plus clairement (ni si c'est juste d'ailleurs). Si tu peux revenir dans 2 ans j'aurai les idées plus claires :marteau: :lol4:

En attendant si yos, tize ou une autre bonne âme pouvait donner leur avis :id:

par **yos** » 12 Déc 2007, 22:52

Bonsoir.
Partir des groupes commutatifs me parait bien.
Pour n=5, il n'y a que Z/5Z et pour n=6, il n'y a que Z/6Z (

est pas abélien).
Pour la multiplication, la distributivité de X sur + te permet de trouver :
2X3=(1+1)X3=...

par **Elvis** » 12 Déc 2007, 22:54

Pour n=6, on ne considère pas Z/3Z x Z/2Z (quoiqu'avec le lemme chinois, c'est isomorphe à Z/6Z) ... ??

par **Elvis** » 12 Déc 2007, 22:58

Par contre, je ne vois pas trop ce que sert de montrer 2x3 = (1+1)x3 = 1x3 + 1x3

D'ailleurs, pour ce qui est de la définition de la loi X à partir du groupe, ça ne change rien si je décide de dire que 3 par ex est élément neutre, ou bien de changer les règles de multiplication ?

par **Elvis** » 12 Déc 2007, 23:02

Ah, c'est pour montrer que dans tous les cas de figure, 2 ne peut pas être élément neutre ?

par **Elvis** » 12 Déc 2007, 23:11

Je viens de penser à un truc. Si je considère les ensembles à 5 éléments.
Les groupe commutatifs : Z/5Z.
Je montre que je ne peux pas définir d'autres éléments neutres (1 est l'unique solution). Donc il n'y a que Z/5Z.
Est ce que c'est à peu près correct ?

par **leon1789** » 12 Déc 2007, 23:34

ceci ne te convient pas ?
http://www.maths-forum.com/showpost.php?p=317137&postcount=8

par **yos** » 13 Déc 2007, 11:35

Elvis a écrit:D'ailleurs, pour ce qui est de la définition de la loi X à partir du groupe, ça ne change rien si je décide de dire que 3 par ex est élément neutre, ou bien de changer les règles de multiplication ?

Dans Z/5Z ça change rien : les éléments 1,2,3,4 sont indiscernables du point de vue de l'addition (tous générateurs). Que tu prennes 1 ou 3 comme élément neutre, tu obtiendras deux fois le même anneau. Par contre dans Z/6Z, il faut regarder.

Elvis a écrit:Par contre, je ne vois pas trop ce que sert de montrer 2x3 = (1+1)x3 = 1x3 + 1x3

Une fois choisi le neutre (il est vrai que je pensais à 1 ici), la table de multiplication tombe non?

par **ThSQ** » 13 Déc 2007, 20:33

En attendant la colle d'anglais ce midi j'ai remis un peu au propre tout ça, et j'ai ajouté un nouvel anneau à 4 éléments ...

Donc pour n=4 : 4 anneaux non isomorphes

A savoir Z/4Z, Z/2Z²,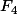

et

un quatrième étrange défini par :
A_4 = { 0, 1, a, b=1+a } avec ab = b, a² = 1, b²=0

Etrange également (mais peut-être y a-t-il une explication plus générale), je n'ai pas trouvé d'anneau non commutatif (unitaire pour lever cette ambigüité énervante) à 4 éléments. :doh:

Algèbre !!

Algèbre !!

Explications pour algèbre

Qui est en ligne