Algebre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
saifert
- Membre Naturel
- Messages: 25
- Enregistré le: 18 Mar 2007, 17:38
-
 par saifert » 09 Juin 2007, 15:31
par saifert » 09 Juin 2007, 15:31
Bonjour,
Je fais des revisions, et je suis tombee sur cet petit exo d'algebre.
Soit G un groupe tel que

pour tout element g de G. Montrer que G est abelien.
Reponse :Comme G est un groupe alors G admet un element neutre e et




(hyp. de l'enonce)
=(b.b).a)
.b=b.(b.a))
(par associativite)
et on a
b=b(b.a)=a)
Alors

et

Comme on sait que l'element neutre d'un groupe est unique, on deduit :
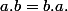
Donc G est abelien.
Je n'ai pas la correction, alors est-ce que qqn pourrai verifier que la demo est correcte ? :hein:
Merci.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Juin 2007, 15:36
par tize » 09 Juin 2007, 15:36
Bonjour,
il y a une erreur dans ton raisonnement je crois, quand tu écris :
saifert a écrit:Alors

et

Sinon tu peux essayer de bidouiller (ab)²=e, ça tombe assez facilement.
-
saifert
- Membre Naturel
- Messages: 25
- Enregistré le: 18 Mar 2007, 17:38
-
 par saifert » 09 Juin 2007, 16:05
par saifert » 09 Juin 2007, 16:05
Salut,
oui, en effet il y a une erreur : je ne peux ecrire a.b=e et b.a=e que si (a.b)b=b(b.a)=b et non quand (a.b)b=b(b.a)=a.
Par contre je ne vois pas comment le resoudre avec
^2=e)
:hein:
Merci de nouveau.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Juin 2007, 16:08
par tize » 09 Juin 2007, 16:08
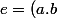^2=ab.ab)
ensuite multiplie par a à gauche et b à droite.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
