Bonjour,
je fais des révisions avec ce poly.
Pas à l'aise avec la Définition 14 (où il doit manquer ∀x∈E). J'aurais préféré qu'on dise: Ker q={x∈E| q(x)=0}. Ainsi, la définition 17 deviendrait q définie <=> Ker q={0}.
La Définition 14 est-elle standard? Si oui, où réside son intérêt?
Algèbre bilinéaire | Phi non-dégénérée, q définie
8 messages
- Page 1 sur 1
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
Salut,
La définition 14 est "on ne peut plus standard" et elle n'est pas du tout équivalente à q(x)=0.
Et son "intérêt", ben c'est le même que celui du noyau d'une application linéaire : si le noyau est réduit à {0}, ta forme quadratique va être dite "non dégénérée" et avoir pas mal de propriétés (par exemple en ce qui concerne la dimension des orthogonaux des s.e.v.) qu'elle n'a pas sinon. Bref, tu as des tonnes de théorème qui vont commencer par "si c'est non dégénéra alors . . ." (*)
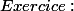 Soit
Soit 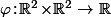 définie par
définie par ;(x',y')\big)\!=xy'\!+\!yx')
a) Montrer que est une forme bilinéaire symétrique. Quelle est la forme quadratique
est une forme bilinéaire symétrique. Quelle est la forme quadratique  associée.
associée.
b) Déterminer le noyau de , c'est à dire
, c'est à dire \!=\!\{X\!\in\!{\mathbb R}^2\text{ t.q. }\forall Y\!\in\!{\mathbb R}^2,\ \varphi(X,Y)\!=\!0\})
c) Déterminer le cône isotrope de c'est à dire
c'est à dire 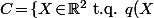\!=\!0\}) . Est-il égal au noyau ? Est-ce un s.e.v. de
. Est-il égal au noyau ? Est-ce un s.e.v. de 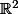 ?
?
Sinon, (mais ça risque d'être un peu théorique pour toi), une forme bilinéaire\mapsto\varphi(X,Y)) sur
sur 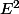 c'est en fait une application linéaire de
c'est en fait une application linéaire de  dans l'e.v.
dans l'e.v. 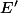 des formes linéaires sur
des formes linéaires sur  (i.e. des applications linéaires de
(i.e. des applications linéaires de  dans le corps de base
dans le corps de base  ). Plus précisément, avec ce point de vue, l'image d'un (et d'un seul)
). Plus précisément, avec ce point de vue, l'image d'un (et d'un seul)  de
de  par
par  , c'est la forme linéaire
, c'est la forme linéaire ) et ce que désigne
et ce que désigne ) c'est le noyau de l'application linéaire (et pas bilinéaire)
c'est le noyau de l'application linéaire (et pas bilinéaire) 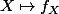 de
de  dans
dans 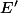 .
.
(*) Et avec le point de vue des applications de E dans E', si tu est en dimension finie et que ta forme quadratique est non dégénérée,elle te fourni un isomorphisme entre E et son dual E'.
La définition 14 est "on ne peut plus standard" et elle n'est pas du tout équivalente à q(x)=0.
Et son "intérêt", ben c'est le même que celui du noyau d'une application linéaire : si le noyau est réduit à {0}, ta forme quadratique va être dite "non dégénérée" et avoir pas mal de propriétés (par exemple en ce qui concerne la dimension des orthogonaux des s.e.v.) qu'elle n'a pas sinon. Bref, tu as des tonnes de théorème qui vont commencer par "si c'est non dégénéra alors . . ." (*)
a) Montrer que
b) Déterminer le noyau de
c) Déterminer le cône isotrope de
Sinon, (mais ça risque d'être un peu théorique pour toi), une forme bilinéaire
(*) Et avec le point de vue des applications de E dans E', si tu est en dimension finie et que ta forme quadratique est non dégénérée,elle te fourni un isomorphisme entre E et son dual E'.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
OK, merci, mais je n'ai pas dit, ni pensé, qu'il y avait équivalence entre Définition 14 et q(x)=0. C'est d'ailleurs l'objet de la Remarque suivant Proposition 18. Je dis qu'il aurait plus simple de définir Ker q={x|q(x)=0} et utiliser un autre nom, par ex, Ker Phi (?) = {y|∀x, phi(x,y)=0}. Dailleurs il semble bien que vous ayez fait cette modification par vous même.
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
Non, sur le principe, ça serait une très mauvaise idée d'appeler le cône isotrope (i.e. l'ensemble des X tels que q(X)=0) le "noyau" de quelque chose : ce terme de noyau est exclusivement réserve aux "morphismes de la structure", c'est à dire dans le cas de l'algèbre linéaire, aux applications linéaires.
Par contre que l'ensemble des X tels que, pour tout Y on ait phi(X,Y)=0, que tu le note Ker(phi) où Ker(q), ça n'a pas grande importance. Effectivement au niveau "pur logique", c'est plutôt Ker(phi) que Ker(q), mais quelque part phi et q c'est plus ou moins "le même objet" (les formules de polarisation te permettent de retrouver phi connaissant q).
Enfin bref, l'ensemble des X tels que q(X)=0 (c'est à dire le cône isotrope), il faut surtout pas commencer à dire que c'est le noyau de quelque chose sinon tu risque de complètement t'emmêler les pinceaux le jour ou tu verra des structures un peu compliquées. (et l'autre intérêt d'appeler ça comme tout le monde un "cône", ben déjà, c'est que dans R^3, c'est effectivement très souvent un cône est aussi que c'est avec des truc du style q(X)=constante qu'on définie les "coniques" : paraboles, ellipses et hyperboles)
Par contre que l'ensemble des X tels que, pour tout Y on ait phi(X,Y)=0, que tu le note Ker(phi) où Ker(q), ça n'a pas grande importance. Effectivement au niveau "pur logique", c'est plutôt Ker(phi) que Ker(q), mais quelque part phi et q c'est plus ou moins "le même objet" (les formules de polarisation te permettent de retrouver phi connaissant q).
Enfin bref, l'ensemble des X tels que q(X)=0 (c'est à dire le cône isotrope), il faut surtout pas commencer à dire que c'est le noyau de quelque chose sinon tu risque de complètement t'emmêler les pinceaux le jour ou tu verra des structures un peu compliquées. (et l'autre intérêt d'appeler ça comme tout le monde un "cône", ben déjà, c'est que dans R^3, c'est effectivement très souvent un cône est aussi que c'est avec des truc du style q(X)=constante qu'on définie les "coniques" : paraboles, ellipses et hyperboles)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
La forme bilinéaire phi induit une forme linéaire dans son dual, dont le noyau est identique à {q(x)=0}. Si cette assertion est vraie, il serait légitime de définir Ker q = {q(x)=0}. Quoiqu'il en soit, la Définition 14 porte à confusion, et il vaut mieux s'en tenir à Ker phi = {x: qqs y, phi(x,y)=0}, où phi forme polaire associée à la forme quadratique q.
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
Ben34, je m'attendais à ce que vous rebondissiez sur mon dernier message dans cette discussion. Vous aurait-il échappé?
Re: Algèbre bilinéaire | Phi non-dégénérée, q définie
Bonjour !
Que veut dire "...induit une forme linéaire dans son dual" ?
L'ensemble des vecteurs isotropes n'est pas, sauf cas particulier, un sous-espace vectoriel : il y a donc peu de chances que ce soit un "noyau" d'application linéaire!
Que veut dire "...induit une forme linéaire dans son dual" ?
L'ensemble des vecteurs isotropes n'est pas, sauf cas particulier, un sous-espace vectoriel : il y a donc peu de chances que ce soit un "noyau" d'application linéaire!
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
