Aide exercice Argth
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
meloman0
- Membre Naturel
- Messages: 12
- Enregistré le: 22 Sep 2010, 22:45
-
 par meloman0 » 22 Sep 2010, 22:51
par meloman0 » 22 Sep 2010, 22:51
Svp je ne sais pas la méthode a suivre pour résoudre cet exercice aidez moi svp. Simplifier l'expression suivante: argth(racine)((chx-1)/(chx+1))

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Sep 2010, 09:13
par Ericovitchi » 23 Sep 2010, 09:13
c'est quoi que tu appelles argth ? arc tan hyperbolique ?
-
mathelot
 par mathelot » 23 Sep 2010, 10:58
par mathelot » 23 Sep 2010, 10:58
bah,
faut exprimer le quotient sous la racine avec du th
on réduit au même dénominateur

et

et trivialement on trouve des carrés parfaits
à la louche, ça fait 2x

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Sep 2010, 12:18
par Ben314 » 23 Sep 2010, 12:18
Salut,
Une méthode un peu bourrin consiste à dériver l'expression (ce qui fait "disparaitre" l'Arg tangente hyperbolique), à simplifer l'expression trouvée de façon à en déduire une primitive "simple"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
meloman0
- Membre Naturel
- Messages: 12
- Enregistré le: 22 Sep 2010, 22:45
-
 par meloman0 » 23 Sep 2010, 22:49
par meloman0 » 23 Sep 2010, 22:49
j'ai pas pu le résoudre donner moi comment vous avez fait svp
-
meloman0
- Membre Naturel
- Messages: 12
- Enregistré le: 22 Sep 2010, 22:45
-
 par meloman0 » 23 Sep 2010, 23:20
par meloman0 » 23 Sep 2010, 23:20
personne ici pour me répondre?
-
flavigny
- Membre Relatif
- Messages: 108
- Enregistré le: 24 Jan 2010, 11:32
-
 par flavigny » 24 Sep 2010, 06:54
par flavigny » 24 Sep 2010, 06:54
Une piste
=\frac{1+\tanh^2(x)}{1-\tanh^2(x)})
-
mathelot
 par mathelot » 24 Sep 2010, 07:52
par mathelot » 24 Sep 2010, 07:52

en écrivant
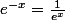
et en réduisant au même dénominateur
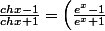^2)
après discuter si x>0 ou x<0

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Sep 2010, 16:34
par Ben314 » 24 Sep 2010, 16:34
Salut,
C'est extrèmement bourrin, mais ça a l'intérêt d'éviter de réfléchir...
-1}{\cosh(x)+1}}\Big))
est continue sur

, dérivable sur

et, pour tout

, on a :
-1}{\cosh(x)+1}}}{1-\Big(\sqrt{ \frac{\cosh(x)-1}{\cosh(x)+1}}\Big)^2}<br />=\frac{\cosh(x)+1}{2}\times\frac{ \frac{\partial}{\partial x}\Big( \frac{\cosh(x)-1}{\cosh(x)+1}\Big)}<br />{2\sqrt{ \frac{\cosh(x)-1}{\cosh(x)+1}}}<br />=\frac{(\cosh(x)+1)^{\frac{3}{2}}}{4(\cosh(x)-1)^{\frac{1}{2}}}\times<br />\frac{\sinh(x)(\cosh(x)+1)-(\cosh(x)-1)\sinh(x)}{(\cosh(x)+1)^2})
}{4(\cosh(x)-1)^{\frac{1}{2}}(\cosh(x)+1)^{\frac{1}{2}}}<br />=\frac{\sinh(x)}{2(\cosh^2(x)-1)^{\frac{1}{2}}}<br />=\frac{\sinh(x)}{2(\sinh^2(x))^{\frac{1}{2}}}<br />=\frac{\sinh(x)}{2|\sinh(x)|}<br />=\left\{\matrix{\ \ \frac{1}{2}&{\rm si }x>0\cr -\frac{1}{2}&{\rm si }x<0 \right.)
Comme
=0)
, cela implique que...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
