15 résultats trouvés
Revenir à la recherche avancée
Bon merci beaucoup, voir ces circulaires réciproques a payé y en avait une au devoir, d'ailleurs une des fonctions plus monstrueuses que j'ai vu (j'ai pas vu grand chose en maths faut dire): F(x)= Arcsin (2x-1)+ 2Arctan sqrt{\frac{1-x}{x}} Grâce à la troisième d'hier (c'est la même chose en ...
- 07 Nov 2013, 16:21
- Forum: ✯✎ Supérieur
- Sujet: étude fonctions circulaire réciproque
- Réponses: 8
- Vues: 1095
Du coup pour la racine, je me retrouve juste avec des valeurs absolues non? ((x²-1)² n'est pas toujours positif même sur mon intervalle d'étude [0;+inf[) Je suis pas trop sûr de quoi en faire mais en fait, puisque qu'au dénominateur j'ai produit d'une expression positive avec une valeur absolue (don...
- 06 Nov 2013, 21:11
- Forum: ✯✎ Supérieur
- Sujet: étude fonctions circulaire réciproque
- Réponses: 8
- Vues: 1095
Merci de tes précisions, même si je t'assure que tout équipement électronique est interdit :/ J'en ai deux autres à faire ce soir (je dois rattraper beaucoup de trucs du fait d'absences, dès que j'ai fini j'enchaine sur d'autres choses T_T), je serais très reconnaissant d'avoir de l'aide car je bloq...
- 06 Nov 2013, 18:15
- Forum: ✯✎ Supérieur
- Sujet: étude fonctions circulaire réciproque
- Réponses: 8
- Vues: 1095
étude fonctions circulaire réciproque
Bonjour, je dois faire l'étude de la fonction f(x)= Arctan ((x^2+1)/x). Je vais afficher la photo de ce que j'ai fait ce sera plus rapide que de recopier: http://img4.hostingpics.net/pics/79326920131106152157.jpg Ma question serait en fait, vu qu'en principe on ne doit pas utiliser la calculatrice, ...
- 06 Nov 2013, 15:39
- Forum: ✯✎ Supérieur
- Sujet: étude fonctions circulaire réciproque
- Réponses: 8
- Vues: 1095
x=sqrt{e^y(2-e^y)} ? (puisque les x de f(x) sont positifs?) Je trouvais une racine sur les deux e différents dessous un peu "moche" comme réponse du coup je pensais qu'il fallait encore transformer même si ça semble pas trop possible. Le graphe de madame calculette semble me dire ...
- 15 Oct 2013, 23:02
- Forum: ✎✎ Lycée
- Sujet: déterminer une fonction réciproque (dm à rendre pour demain)
- Réponses: 3
- Vues: 603
(désolé du double post, c'est pour marquer mon avancée par rapport au edit)
J'en arrive donc à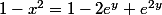 , mais je suis encore coincé...
, mais je suis encore coincé...
edit: je trouve en bidouillant) , mais je suis pas trop avancé en fait
, mais je suis pas trop avancé en fait
:[
J'en arrive donc à
edit: je trouve en bidouillant
:[
- 15 Oct 2013, 22:41
- Forum: ✎✎ Lycée
- Sujet: déterminer une fonction réciproque (dm à rendre pour demain)
- Réponses: 3
- Vues: 603
déterminer une fonction réciproque (dm à rendre pour demain)
Bonsoir, j'ai du mal avec la dernière question de mon dm, il faut trouver la fonction réciproque de f(x)=ln(1-sqrt{1-x^2}) , qui est bijective si l'ensemble de départ est ]0;1] et celui d'arrivée R-. Je sais trouver une fonction réciproque y=f(x) x=f(y) mais avec des fonctions simple...
- 15 Oct 2013, 22:22
- Forum: ✎✎ Lycée
- Sujet: déterminer une fonction réciproque (dm à rendre pour demain)
- Réponses: 3
- Vues: 603
- 15 Oct 2013, 21:54
- Forum: ✎✎ Lycée
- Sujet: Finir un DM à rendre pour demain (étude de fonction), besoin
- Réponses: 3
- Vues: 776
Finir un DM à rendre pour demain (étude de fonction), besoin
Bonsoir, dans un exercice sur le DM, j'en arrive à tracer cette courbe http://img11.hostingpics.net/pics/47284820131015220322.jpg de la fonction f(x)= x^2 + x + 1 -3lnx. (définie sur ]0;+inf[) [edit: attention j'ai oublié de pivoter l'image, l'axe des ordonnées est celui qui est à l'horizontale sur ...
- 15 Oct 2013, 21:17
- Forum: ✎✎ Lycée
- Sujet: Finir un DM à rendre pour demain (étude de fonction), besoin
- Réponses: 3
- Vues: 776
Le principe est simple à appliquer mais le concept en lui-même me semble compliqué. Car du coup, quand on met au carré on a un parti-pris non? (on raisonne par implication et pas par équivalence si j'ai bien saisi), et pour les cas où 1-x serait <0 on ne peut rien vérifier/résoudre? C'est un peu tor...
- 12 Oct 2013, 22:26
- Forum: ✎✎ Lycée
- Sujet: équation second degré avec racine carrée
- Réponses: 5
- Vues: 1120
D'accord merci, mais du coup je bute pour le lien avec l'identité remarquable. C'est parce-qu'il y a trois éléments (a+b)*(a+b)*(a+b) et que ça représenterait toutes les combinaisons possibles? Bon je saisis pas bien vu qu'à l'intérieur il y a deux éléments. edit: pour certaines raisons j'ai zappé l...
- 12 Oct 2013, 22:17
- Forum: ✎✎ Lycée
- Sujet: Énumérer les parties d'un ensemble
- Réponses: 8
- Vues: 3474
J'avoue que j'ai du mal avec toute la terminologie. Je suppose que votre 2) et 3) présentent un ensemble à 2 et 3 éléments. Donc je dirais sans trop de conviction que pour un ensemble à 1 élément il y a 2 parties/sous-ensembles {a} et {vide}. Pour un ensemble à deux éléments 4 parties {a;b}, {a}, {b...
- 12 Oct 2013, 22:07
- Forum: ✎✎ Lycée
- Sujet: Énumérer les parties d'un ensemble
- Réponses: 8
- Vues: 3474
Pourtant si je tape sur la calculette x+sqrt{3x-1}-1 (et non x^2-5x+2 où j'étais arrivé), la courbe ne coupe en aucun cas l'axe des abscisses pour une valeur aussi grande que x2. C'est bizarre non :/? même si je sais bien qu'en partant de là x peut prendre moins de valeurs, de là à changer complètem...
- 12 Oct 2013, 21:46
- Forum: ✎✎ Lycée
- Sujet: équation second degré avec racine carrée
- Réponses: 5
- Vues: 1120
Énumérer les parties d'un ensemble
J'ai un exo (sans leçon) censé faire appel à des acquis (je suis en term) mais je ne le comprend pas: 1.Enumérer les parties d'un ensemble à 1 élément. 2.Énumérer les parties d'un ensemble à 2 éléments. 3.Énumérer les parties d'un ensemble à 3 éléments. 4.Énumérer les parties d'un ensemble à 4 éléme...
- 12 Oct 2013, 21:19
- Forum: ✎✎ Lycée
- Sujet: Énumérer les parties d'un ensemble
- Réponses: 8
- Vues: 3474
équation second degré avec racine carrée
Bonjour, j'ai un petit souçis pour trouver la méthode avec une équation du second degré: x+sqrt{3x-1}=1 Moi j'ai juste mis le x de l'autre coté puis tout mis au carré ce qui fait 3x-1 = 1-2x+x^2 donc au final x^2-5x+2=0 je trouve deux racines x1=\frac{5-sqrt{17}}{2} x2=\frac{5+sqrt{17}}{2} j'ai véri...
- 12 Oct 2013, 21:12
- Forum: ✎✎ Lycée
- Sujet: équation second degré avec racine carrée
- Réponses: 5
- Vues: 1120
- 15 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
