Bonsoir à tous,
J'ai un exercice à faire sur des triangles équilatéraux directs (dans le plan complexe) mais je n'arrive pas à aboutir au résultat. Je pense avoir trouver un piste mais pas plus...
Voici l'énoncé :
Soit ABC un triangle direct (l'angle des vecteurs AB et AC est direct). Soit A', B' et C' trois points tels que les triangles A'CB, B'AC, C'BA soient directs.
1/ Le plan est dans un repère (o,i,j). Exprimer a', b' et c' à l'aide de a, b, c (affixes des points). On pourra utiliser j=exp(2i;)/3).
2/ On considère les points M,N,P les centres de gravités des triangles A'CB, B'AC et C'BA.
Déterminer les affixes m, n, p.
Alors voici quelques pistes que j'ai envisagées.
Pour la question 1,
on a a'=ub+w
et a'=uc+w
on a c'=ua+w
et c'=ub+w
on a b'=ua+w
et b'=uc+w
Mais à ce niveau, je ne vois pas comment exprimer les affixes à l'aide de j.
Pour la question 2, je pensais utiliser la définition du centre de gravité et des médianes.
Le centre de gravité est au deux-tiers des médianes à partir des sommets. Il faut donc calculer le milieu du côté opposé pour trouver l'affixe du vecteur.
Par ailleurs, comment exprimer les affixes des points A, B et C avec j ?
Il faut juste écrire A=xa+ya*i ?
Merci davance pour votre aide,
Reynolds
Triangles équilatéraux directs
9 messages
- Page 1 sur 1
Il ne manquerais pas par hasard un petit bout d'énoncé, par exemple :
Reynolds_05 a écrit:Voici l'énoncé :
Soit ABC un triangle direct (l'angle des vecteurs AB et AC est direct). Soit A', B' et C' trois points tels que les triangles A'CB, B'AC, C'BA soient équilatéraux directs.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Rappel : un triangle PQR est équilatéral direct ssi 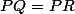 (longueurs) et l'angle de
(longueurs) et l'angle de 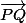 vers
vers 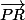 vaut
vaut 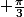
Si les points P,Q,R ont pour affixe , tu doit savoir exprimer les longueurs
, tu doit savoir exprimer les longueurs 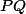 et
et  ainsi que l'angle de
ainsi que l'angle de 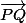 vers
vers 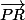 à l'aide de
à l'aide de 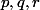 et en déduire que PQR est équilatéral direct ssi
et en déduire que PQR est équilatéral direct ssi 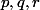 vérifient ...
vérifient ...
Si les points P,Q,R ont pour affixe
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Rappel : un triangle PQR est équilatéral direct ssi(longueurs) et l'angle de
vers
vaut
Si les points P,Q,R ont pour affixe, tu doit savoir exprimer les longueurs
et
ainsi que l'angle de
vers
à l'aide de
et en déduire que PQR est équilatéral direct ssi
vérifient ...
La longueur
Donc
Et l'angle de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
