Pavage apériodique du plan par deux triangles rectangles

[Jean_Luc]

Oui, il faudrait faire un petit résumé, tu as raison :lol3:
(j'essayerai de faire ça demain)

@mathlot:

Je ne comprends pas bien ton nouveau choix d'angle, pourrais-tu me décrire ceci un peu mieux (en me donant ) ?
Merci.

[mathelot]

J'ai fait un petit dessin jusqu'à n=5 , le moment ou les hauteurs se "connectent".

re,

1)
On a considéré un grand triangle rectangle , d'angles complémentaires
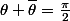
(étape 1)

et et tracé des pieds de hauteurs de manière itérative.

2)
à l'étape 5, on montre par le calcul que certaines hauteurs se "connectent".
3) A une étape n, on donc triangles , tous semblables et semblables au triangle initial. En effaçant certains hauteurs,notamment dans les coins, et en complétant d'autres,on peut se ramener à paver le triangle initial par uniquement deux triangles, dont les aires sont dans un rapport de .

4) on a un effet de "zoom", un effet "fractal", puisque le triangle initial ABC
se retrouve en petit , en son intérieur, semblable par une similitude
d'angle (triangle 11-14-16)

5) Le procédé inverse du "zoom", l'expansion, permet à partir d'un petit triangle 11-14-16 , de l'inclure dans un grand triangle, et donc de paver l'intégralité du plan, par uniquement deux triangles. c'est à ce propos
que l'on a écrit que l'on avait deux classes d'isométrie.

6) On a montré que ces pavages sont a-périodique et que l'angle est incommensurable avec .La démonstration de cette dernière propriété utilise les polynômes de Tchebytcheff.

Je ne sais si tu trouveras ces pavages dignes d'intérêt. On aimerait bien les classer, décrire les procédés d'expansion possibles, trouver d'autres angles
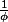
donnant d'autres pavages apériodiques. Pour l'instant, le cosinus de l'angle de base est , , le nombre d'or étant un nombre algébrique de polynome minimal .
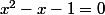
On va essayer de regarder ce que donne d'autres cosinus, en considérant
des exemples de nombres algébriques plus compliqués. Par exemple,
, est un nombre algébrique de polynôme minimal .



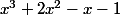
Idéalement, celui qui pave le plan par un seul motif au lieu de deux, finit dans le guiness book ou avec la médaille Fields. :zen:

Pour JL,

Peux tu faire un dessin avec les angles
, tel que et

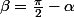
Je ne sais comment tout cela est programmé en Java. Pars-tu d'une valeur approchée des angles ? Si on pouvait avoir un algorithme d'expansion au lieu d'un algorithme de division.. ça , ça a l'air difficile.


PS: la subdivision en triangles donne une illustration des coefficients du binôme, par les aires.