Equation de degré 5 en première S

[carla1996]

Bonjour,
J'ai un DM où je dois résoudre l'équation suivante: 2x^5 + 5x + 2=0.
Je ne vois pas quel changement de variable il faut faire (si c'est comme ca qu'il faut procéder) ou s'il faut utiliser une autre méthode?
Les chapitres sur lesquels on a travaillé sont généralités sur les fonctions et équation du second degré.
Merci d'avance

[Carpate]

Bonjour,
J'ai un DM où je dois résoudre l'équation suivante: 2x^5 + 5x + 2=0.
Je ne vois pas quel changement de variable il faut faire (si c'est comme ca qu'il faut procéder) ou s'il faut utiliser une autre méthode?
Les chapitres sur lesquels on a travaillé sont généralités sur les fonctions et équation du second degré.
Merci d'avance

Je ne vois pas de racine réelle évidente (l'équation admet 4 racines complexes et une racine réelle)
Je suppose que l'on te demande de montrer que l'équation admet une seule racine (réelle) et de donner son encadrement ; donc d'étudier les variation de

[keofran]

A mon avis il y a une erreur d'énoncé, c'est un exposant 2 au lieu du 5.
Avec un degré 2, la méthode du discriminant donne des résultats simples.

[WillyCagnes]

Je ne vois pas de racine réelle évidente (l'équation admet 4 racines complexes et une racine réelle)
Je suppose que l'on te demande de montrer que l'équation admet une seule racine (réelle) et de donner son encadrement ; donc d'étudier les variation de

bonjour,

calcule f(0) et f(-1)
un changement de signe d'ou la racine réelle est comprise entre -1 et 0

[Carpate]

bonjour,

calcule f(0) et f(-1)
un changement de signe d'ou la racine réelle est comprise entre -1 et 0

Ca serait bien si Carla1996 daignait répondre à la question : est-ce ou dans l'équation proposée ?

[chombier]

bonjour,

calcule f(0) et f(-1)
un changement de signe d'ou la racine réelle est comprise entre -1 et 0

1ère S -> pas de TVI

Je vote pour une erreur d'énoncé

[carla1996]

Je vous remercie pour vos réponses, c'est peut être effectivement une erreur d'énoncé mais j'ai encore un doute car c'est pour un DM de difficulté croissante et ca fait partie de la dernière équation (avant il y avait des changement de variables...ect)
Merci encore je vous tiendrais au courant!

[busard_des_roseaux]

est-ce que cette équation de degré 5 a un rapport avec les questions précédentes ?

trace les courbes d'équation et la droite d'équation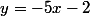

Elles n'ont qu'un point d'intersection d'abscisse

Quand on remplace x par 0 et -1 , on trouve deux images de signes opposés, si bien que l'on est sûr que le polynome s'annule

d'apès une théorie de post-bac, la fonction polynome
est le produit d'une fonction affine et de deux trinomes de discriminant strictement négatifs

[Black Jack]

2x^5 + 5x + 2=0.

f(x) = 2x^5 + 5x + 2

f'(x) = 10.x^4 + 5 > 0 pour tout x et donc f(x) est strictement croissante sur R.
lim(x--> -oo) f(x) = -oo
lim(x--> +oo) f(x) = +oo

Des 3 lignes précédentes, on peut conclure qu'il y a une et une seule valeur réelle alpha de x telle que f(x) = 0

f(-1) = -2-5+2 = -5 < 0
f(0) = 2 > 0

alpha est dans ]-1 ; 0[ et comme f(x) est monotone, on peut approcher la valeur de alpha avec la précision qu'on veut (sauf valeur exacte) par exemple par approximations successives en utilisant la méthode dichotomique.
*****

:zen:

[busard_des_roseaux]

et comme f(x) est monotone

f est monotone sur l'intervalle R