Résolution équation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 16:15
par ViolaineV » 29 Sep 2013, 16:15
Bonjour, il m'est demandé dans un exercice de trouver les valeurs de x et y tels que 25x²=y²+2017
J'en ai donc conclut qu'il fallait résoudre 25x²-y²+2017=0, mais je suis bloquée ici car je n'arrive pas à résoudre une équation du second degré à deux inconnues.
Merci de votre aide.
-
marysia1996
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Sep 2013, 15:55
-
 par marysia1996 » 29 Sep 2013, 16:17
par marysia1996 » 29 Sep 2013, 16:17
il faut faire un système
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 16:26
par mcar0nd » 29 Sep 2013, 16:26
Salut, tu veux résoudre

, donc tu te retrouves avec

.
Tu factorise le membre de droite avec l'identité remarquable

. ET qu'est ce que tu peux dire à propos de 2017, de ses diviseurs notamment?
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 16:27
par ViolaineV » 29 Sep 2013, 16:27
Merci, je vais essayer.
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 16:29
par ViolaineV » 29 Sep 2013, 16:29
mcar0nd a écrit:Salut, tu veux résoudre

, donc tu te retrouves avec

.
Tu factorise le membre de droite avec l'identité remarquable

. ET qu'est ce que tu peux dire à propos de 2017, de ses diviseurs notamment?
Je dois seulement trouver la valeur de x et y pour que 25x^2=y^2+2017.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 16:31
par mcar0nd » 29 Sep 2013, 16:31
ViolaineV a écrit:Je dois seulement trouver la valeur de x et y pour que 25x^2=y^2+2017.
Oui, suis ce que je t'ai dit dans mon premier message et tu devrais y voir plus clair.

-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 16:34
par ViolaineV » 29 Sep 2013, 16:34
mcar0nd a écrit:Oui, suis ce que je t'ai dit dans mon premier message et tu devrais y voir plus clair.

D'accord, j'essai merci

-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 16:45
par ViolaineV » 29 Sep 2013, 16:45
Malgré ton aide avec l'identité remarquable, je suis bloqué car il y a deux inconnues et je ne sais vraiment pas comment m'y prendre :/
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 16:50
par mcar0nd » 29 Sep 2013, 16:50
ViolaineV a écrit:Malgré ton aide avec l'identité remarquable, je suis bloqué car il y a deux inconnues et je ne sais vraiment pas comment m'y prendre :/
Est ce que tu as réussi à factoriser?
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 17:05
par ViolaineV » 29 Sep 2013, 17:05
mcar0nd a écrit:Est ce que tu as réussi à factoriser?
Oui 25x^2-y^2=(25x+y)(25x-y)
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 17:06
par mcar0nd » 29 Sep 2013, 17:06
ViolaineV a écrit:Oui 25x^2-y^2=(25x+y)(25x-y)
Hum attention, c'est
(5x-y))
étant donné que
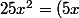^2)
.
Donc maintenant, qu'est ce que tu peux dire de 2017, quels sont ces diviseurs?
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 17:14
par ViolaineV » 29 Sep 2013, 17:14
mcar0nd a écrit:Hum attention, c'est
(5x-y))
étant donné que
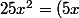^2)
.
Donc maintenant, qu'est ce que tu peux dire de 2017, quels sont ces diviseurs?
Les diviseurs de 2017 sont 1 et 2017.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 17:15
par mcar0nd » 29 Sep 2013, 17:15
ViolaineV a écrit:Les diviseurs de 2017 sont 1 et 2017.
Exact, donc 2017 peut uniquement s'écrire

.
Qu'est ce que tu en déduis quant à la résolution de l'équation
(5x+y)=2017)
?
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 17:19
par ViolaineV » 29 Sep 2013, 17:19
mcar0nd a écrit:Exact, donc 2017 peut uniquement s'écrire

.
Qu'est ce que tu en déduis quant à la résolution de l'équation
(5x+y)=2017)
?
Je suis pas sure mais si 2017 est divisible par 1 et 2017 alors (5x+y)(5x-y) doit être divisible par 1 et 2017 non ? Sinon je n'ai pas compris où tu veux en venir..
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 17:25
par mcar0nd » 29 Sep 2013, 17:25
ViolaineV a écrit:Je suis pas sure mais si 2017 est divisible par 1 et 2017 alors (5x+y)(5x-y) doit être divisible par 1 et 2017 non ? Sinon je n'ai pas compris où tu veux en venir..
C'est pas tout à fait ça.
En fait, 2017=1*2017.
Donc, tu vas avoir 5x+y=1 et 5x-y=2017
ou
5x+y=2017 et 5x-y=1.
Donc 2 systèmes à résoudre.
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 17:39
par ViolaineV » 29 Sep 2013, 17:39
mcar0nd a écrit:C'est pas tout à fait ça.
En fait, 2017=1*2017.
Donc, tu vas avoir 5x+y=1 et 5x-y=2017
ou
5x+y=2017 et 5x-y=1.
Donc 2 systèmes à résoudre.
Ah mais d'accord, je comprenais l'histoire du système tout à l'heure ^^
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 17:45
par mcar0nd » 29 Sep 2013, 17:45
ViolaineV a écrit:Ah mais d'accord, je comprenais l'histoire du système tout à l'heure ^^
Une fois que tu as résolu les systèmes, tu vérifies que ce que tu as trouvé fonctionne et tu conclus sur les couples (x;y) solutions.

-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 17:48
par ViolaineV » 29 Sep 2013, 17:48
mcar0nd a écrit:Une fois que tu as résolu les systèmes, tu vérifies que ce que tu as trouvé fonctionne et tu conclus sur les couples (x;y) solutions.

Merci beaucoup pour ton aide !
-
ViolaineV
- Membre Naturel
- Messages: 15
- Enregistré le: 06 Mai 2013, 20:10
-
 par ViolaineV » 29 Sep 2013, 18:30
par ViolaineV » 29 Sep 2013, 18:30
ViolaineV a écrit:Merci beaucoup pour ton aide !
Vu que y a un des deux systèmes qui ne marchent pas, les solutions sont x=201.8 et y=-1008 ?
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 29 Sep 2013, 19:35
par mcar0nd » 29 Sep 2013, 19:35
ViolaineV a écrit:Vu que y a un des deux systèmes qui ne marchent pas, les solutions sont x=201.8 et y=-1008 ?
Si y=1008, ça fonctionne aussi. Tu dois trouver 2 couples (x;y) solutions je crois (201,8 ; -1008) et (201,8 ; 1008).

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
