Resolution d'equation diff

[bastien83]

(1) y'+2y=
a est un reel et u est la fonction def sur R par

determiner a pour que u soit solution de (1)

je ne vois pas comment m'y prendre merci d'avance

[Zebulon]

Bonjour,
supposons que u soit une solution de l'équadiff 1,
alors (2).
Calculez u'(x) et déduisez a de l'égalité 2.

[bastien83]

2 petites question :

- pkoi apres l'equation vouis mettez (2) et non (1)
- comment voulez vous que je calcule u'(x) vu que je connais pas u(x)


?????

[Zebulon]

2 petites question :

- pkoi apres l'equation vouis mettez (2) et non (1)
- comment voulez vous que je calcule u'(x) vu que je connais pas u(x)


?????

On peut calculer u' car a est une constante donc .

(2) c'est l'équation (1) avec u, mais à la limite, oubliez (2) et par équivalences en partant de (ça marche même par équivalences) pour arriver à une condition sur a.

[bastien83]

heu....mais comment je fais pour calculer a dans



etant donné que je ne connais pas u'(x)

je nage

[Zebulon]

On peut calculer u' car a est une constante donc .

Quelle est la dérivée de ?
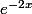
P.S.: Don't worry, vous allez comprendre!

[bastien83]

Quelle est la dérivée de ?
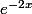
P.S.: Don't worry, vous allez comprendre!

la derivée est :

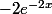
[Zebulon]

la derivée est :

Je vois bien que vous n'avez pas écrit (il faut mettre des accolades car TEX n'aime pas le signe - après la balise).
OK, c'est bien ça. Et que peut-on dire de la dérivée d'une fonction , avec k un réel, en fonction de f'(x)? Par exemple, comment calculez-vous la dérivée de ?

[bastien83]

Je vois bien que vous n'avez pas écrit (il faut mettre des accolades car TEX n'aime pas le signe - après la balise).
OK, c'est bien ça. Et que peut-on dire de la dérivée d'une fonction , avec k un réel, en fonction de f'(x)? Par exemple, comment calculez-vous la dérivée de ?

pour calculer


je ferais (u'*v-u*v')/v² :hum: :hum:

[Zebulon]

OK. On va redémontrer ce résultat alors.

Proposition :
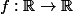
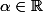
Soit une fonction dérivable sur , soit et soit .
Alors g est dérivable sur I et pour tout x dans I (ou si vous préférez les formules : ) .

Pour la démonstration, posez , et utilisez la formule de dérivation d'un produit.

[bastien83]

desolé mais la je suis à la rue mais complet.
je reprend:
pour trouver le a de u , solution de y'+2y=
je dois trouver la derivée de u'(x) qui est :



dc a=

la redaction c'est pas trop ca mai est ce que le resultat est juste?

[Zebulon]

Non, ce n'est pas juste : a est une constante.

donc vous comprenez ça ou pas?
Ensuite, comme u est solution de 1, on a :

Vous remplacez u'(x) et u(x) dans cette équation et vous en déduisez a.

[bastien83]

j'ai remplacé u'(x) par
et u(x) par
mais maintenat j'ai un petit probleme
est ce que =???

[Zebulon]

Je vous ai dit que :

[bastien83]

j'ai dc


et la je jsuis un poco perdu

[bastien83]

j'ai voulu derivée
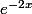
mais ds ce cas le facteur de a =0

[Zebulon]

Oups! J'ai oubié des x! C'est donc .
Et quand on l'introduit dans 1, ça donne?

P.S.: Rien de sert de factoriser, il faut simplifier à point...

[bastien83]

d'apres cette fable, je ne vois pas comment trouver a

[bastien83]

depuis hier soir je cherche mais rien ne viens
si quelqu'un pourrait m'aider

[Dominique Lefebvre]

SI vous le permettez tous les deux, je viens donner un coup de main à Zeb pour t'expliquer cela:

1 - u(x) sera une solution de l'équation différentielle si:

u'(x) + 2*u(x) = 2*exp(-2x) tu es d'accord Bastien?

2 - il faut calculer la dérivée de u(x)

Si u(x) = ax*exp(-2x), on a affaire à une fonction composée que l'on peut écrire f*g tel que f = ax et g = exp(-2x)

Tu sais sans doute que (f*g)' = f'*g + f*g' D'accord jusque là?

Donc tu peux calculer la dérivée de u(x):

u'(x) = (ax)'*exp(-2x) + ax*(exp(-2x))' Tu peux nous calculer ça Bastien?

Ensuite, tu remplaceras dans ton équation différentielle les termes u et u' par leur expression et tu identifies termes à termes.

D'abord, quelle valeur obtiens-tu pour u'(x)?